
不知道大家在幼儿园里有没有玩过这种钢管地球仪?我发现用积木很难搭这种大玩具。特别是在“合法”的前提下!

拼地球仪理所当然应该要用上十字轴和轴的连接件。乐高的轴栓连接件通常两边各连一根轴,中间垂直方向再连一根可以自由旋转角度的栓。乐高有六种不同角度的固定连接件,加上只有一根轴的 0° 件就是七种。现在各厂牌也制造同样的轴栓连接件。这些是常用的固定角度连接件。


此外还有一些三、四轴的连接件。这些零件通常较少见。

6611 和 7329 都是 2025 年才出现的。各只有一个套装用上这种零件。
年初我才设计了几种做时钟钟面的方法。10288、57585 与 32034 搭配可以做出套装 10274 的 12 吊舱摩天轮。这是 12 等分最正确的制作方法之一。因为我只有两个 10288 零件,还没有 57858,先不讨论这个结构。
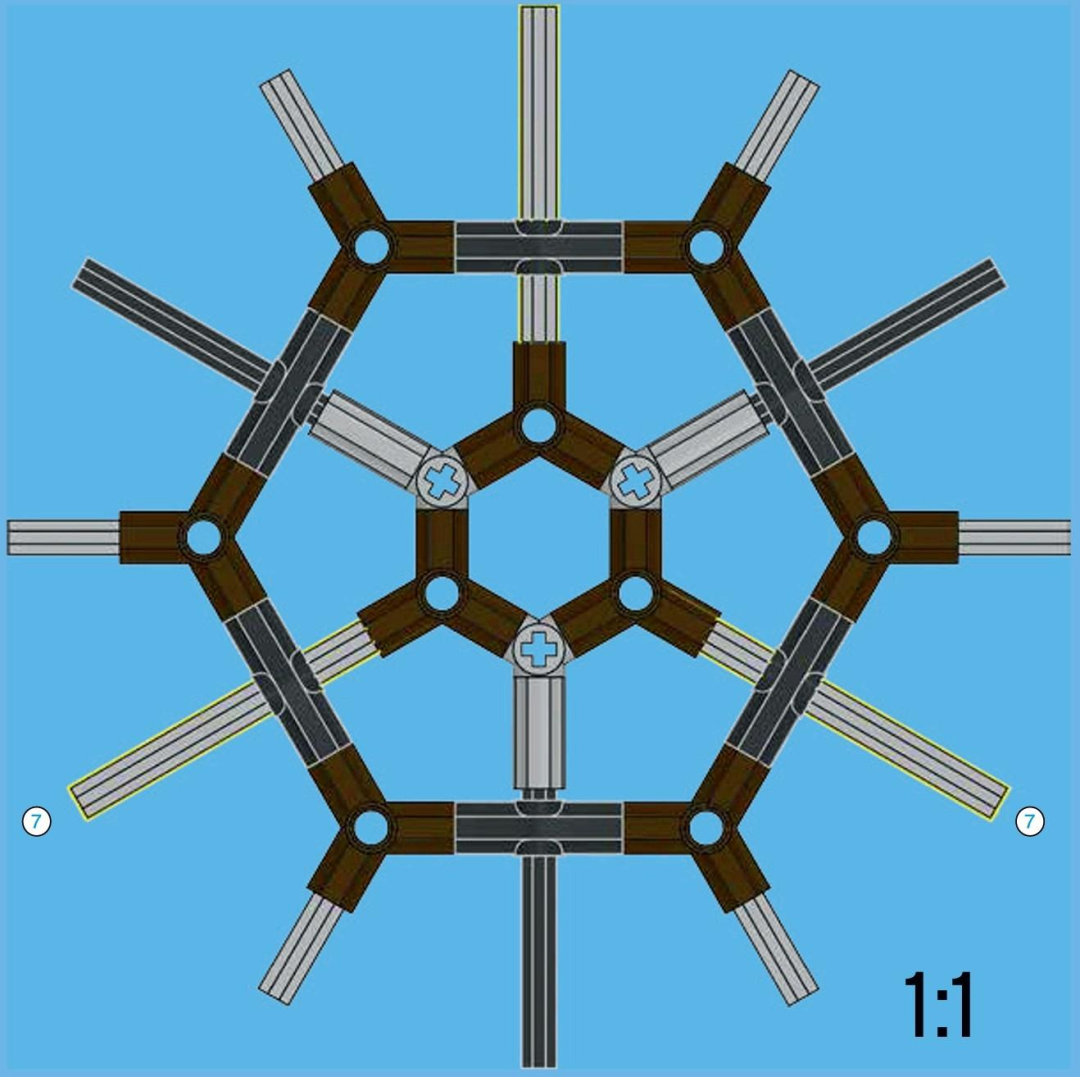
用眼睛看,有时不容易判断连接件的角度。为了方便辨认,乐高还件上标示从 1 到 7 的系列内部号码。这里称为简号。各厂牌的国产零件有些有标示,有些没有。有都不一定看得清楚,没有就真的麻烦大了。
下图是一些国产积木的 2 号件。上面一排没标明制造商,只标了几乎没用的工厂模具号码。90° 和 180° 问题不大。这个系列的其他零件才特别难分辨。
下左的零件标了正确的 2 号。但是橙色和灰色有点不清楚。下右的零件外观干干净净,什么都没标示。这家公司制造的其他零件也让人看了一个头两个大。

二轴连接件的角度从 90° 到 180°,没有锐角。使用相同角度的连接件可以拼出 4, 5, 8, 16, 30 边形。很不幸,不包含 6 和 12 边形。
我有这个系列 7 号以外的所有零件。上排是有正确简号的 Cada 产品。很怪的是,包括乐高都没标示本系列的 1 号件。下排灰、黑、白分别是乐高、不明厂牌,以及 CaDa。三者都没标示 1 号。仔细检验白色件,还会看到一点很小的误差,以至于有一侧插在凸点上不太稳固。这是几年前买的零件。错误很可能后来就改了。

7 号连接件是 2024 年推出的。到 2025 年上半年,还只出现在 9 个套装之中。
这 7 种连接件的 3 到 7 号都能制作正多边形。因为不明原因,5 号和 7 号的角度比理想值稍大,但是都可以接受。
例如用 5 号连接件做 5 边形,会因为连接件角度略大而需要用一点暴力解决。这限制了 5 边形的最小尺寸。暴力应该在塑料的塑性变形范围内,拆开还是可以恢复原状。

乐高也设计了可调角度的连接件,但是我现有的连接件无法锁定角度,所以很少用。这种不能锁定角度的连接件无法制作 6 等分或 12 等分的多边形。

以下是几种多边形和积木可用的角度连接件解决方案。很多必须用其他零件完成。
利用角连接件可以做出下图的 4 种正多边形。为了拼时钟的钟面,还可以再加上一种有点勉强的 12 边形。

因为 12 边形是用两种不同角度的角组合成的,相邻的两个角与中心形成的夹角就不完全相同。用数学可以证明。既然零件还很多,就不妨实际做出来比较。
下图的两个 12 边形,上面的顺时针方向转 2 格,下面的转 1 格。两个 12 边形各在 157.5° 的角上重叠。很容易就能发现,10、11 点方向的四个角不重叠。这是因为不同角度硬组成的 12 边形不是正 12 边形。但这已经是用这种零件所能做到最好的结果了。

轴栓连接件可以做出平面的正多边形,也可以把三个相同的正多边形互相直交成为一个空心球体的骨架。用几何学的术语讲,就是三个互相垂直的大圆。例如说是地球仪上的赤道大圆以及通过经度 0° 和 90° 的两个子午线大圆。
用 8 边形可以勉强做出很简陋的地球仪。这是我现在唯一可以做的东西。
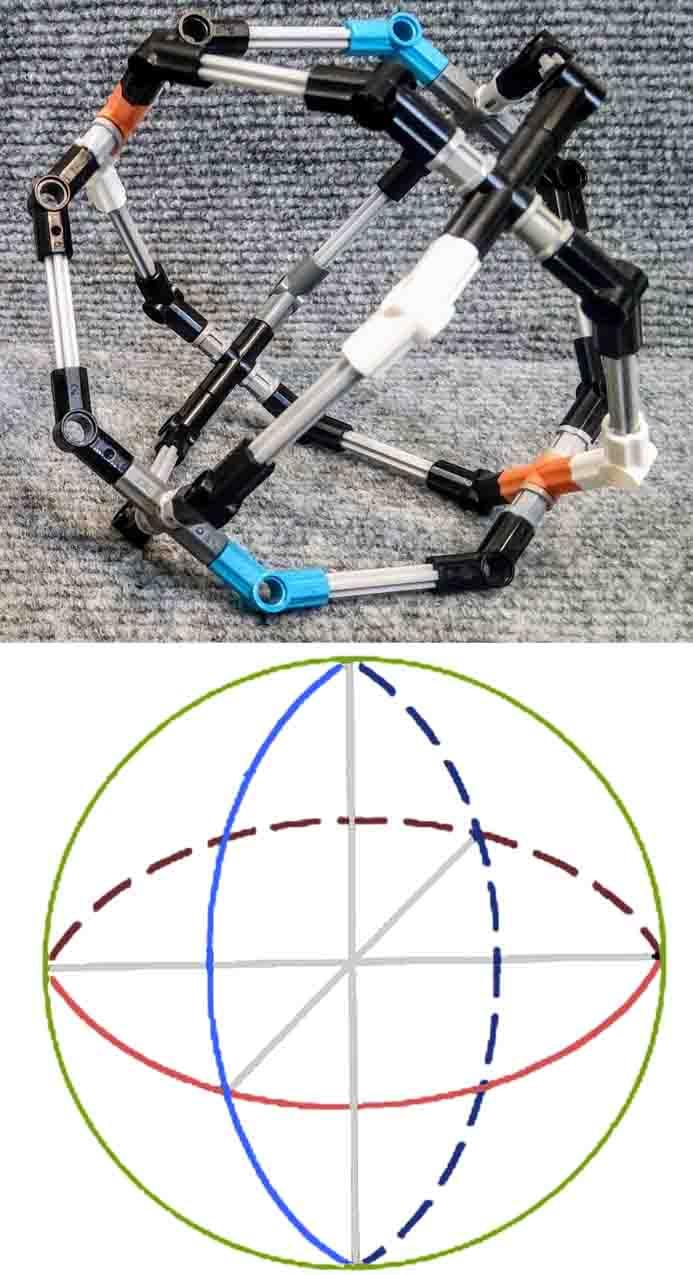
有了多边形,还可以做出多边形的柱。不管几边形都可以用垂直方向的轴拉高变成柱状体。这里用 5 边形示范,其他形状也可以照方抓药。

正多边形有边还有角。上图的两个正 5 边形的边角都连接,看起来很密集。两个正多边形可以边对边连接,也可以角对角连接。

如果允许轴弯曲、扭曲,甚至还可以边对角连接。可能已经犯法了,看不下去就来抓我啊。

连接角的时候,因为对的是圆的插销孔,必须用轴套在孔的两端迫紧连接件,避免连接件移动或是掉出来。因此轴会突出轴套的厚度。这不一定是坏事,但总是可以设法解决这个问题。
用有挡片的轴可以解决挡片一侧的轴套突出问题。但是没有挡片的另一侧轴套仍然会突出。要完全解决问题,可以在另一端也换有挡片的轴,中间用延长轴的联轴器连接。

- 假设两个多边形的距离是n,
- 两边突出轴套的轴长 = n + 4
- 一边突出轴套的轴长 = n + 3
- 两根挡片轴的总轴长 = n + 2
使用两根长度为p, q的挡片轴组合成一根轴,只要满足p + q = n + 2 就可以。

一个足球可以拆分为 12 个 5 边形和 20 个 6 边形。5 边形可以用 60 个连接件制作。6 边形有点麻烦。比较偷懒的方法是在 5 边形的边上做直角方向的辅助线。三根辅助线再交会于 120° 的连接件上,如同下图所示。用 20 个 120° 的连接件就可以做出 20 个 6 边形的中心点。
这个偷懒的方法舍弃了 6 边形的部分外围轮廓(下图紫色细线)。除非特制弹性零件,我们没办法用乐高零件连接两个 5 边形不共平面的顶点。这是无可奈何的。

用类似的方法还可以连接 3 个 8 边形组成的球的“球面”。但是效果不太好。因为 120° 的连接件是在正 8 面体的面上,无法产生曲面感。

连接件的另一个玩法是做成(左)波浪或者是(右)每串联一节就转 90° 的螺旋。

这种螺旋的问题是连接件的轴相对螺旋的轴是歪斜线。插上轴以后会歪歪扭扭转,而不是沿着黄色的螺旋轴转。最简单的解决方法就是把底磨平,用胶粘上转轴或是转盘。角度不容易抓。可能要多牺牲几个才能成功。

最后一个不知道有什么用的设计是两个 5 边形一正一反彼此垂直拼搭。A 的顶点过 B 的底边,B 的顶点过 A 的底边。

红色 5 边形的顶点朝上,绿色 5 边形的顶点朝下。

拼出来这种东西,但是不知道有什么用途。现在终于知道为什么很少人用轴和角度连接件做结构了。











评论留言