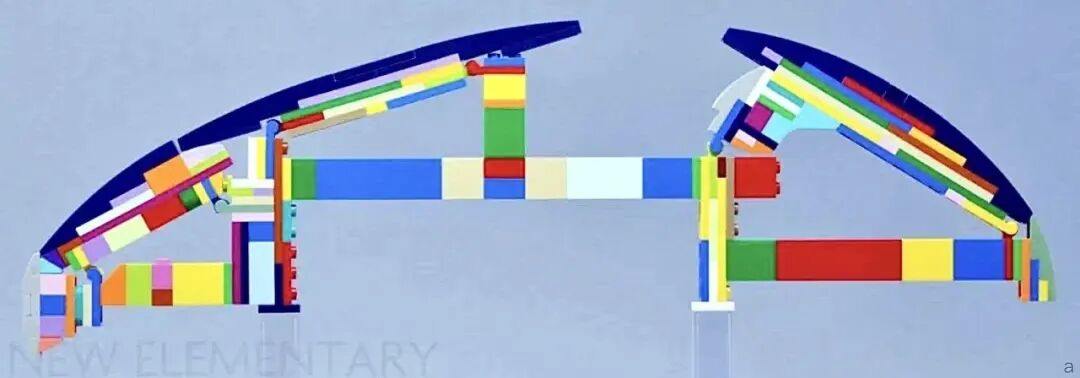
在 2025 年新推出的官方套装——75409 詹戈费特的喷火级飞船中,椭圆形船体结构的搭建方法令人叹为观止。
比起过去推出的体型较小的 75433 詹戈费特飞船,新版本的飞船不再使用简单的弧形零件堆砌,而是使用了一种高阶的搭建技巧:斜面搭建中的砖块勾股结构。

右侧新推出的“熨斗”飞船明显比 75433 更加圆润
然而,我们的老朋友 CTR 常子发现,由于板、轴,和砖之间复杂的换算关系,这种砖块勾股结构十分容易产生非法拼搭。今天,我们就跟随 CTR 常子的脚步,一起计算这三种结构是否合法!
但是在开始之前,我们需要先记住这几个人人皆知的非常非常简单的乐高小公式,它们能帮助我们换算螺柱 stud、板 plate,和活动关节 joint之间的关系:
1、2 stud=5 plate(2s=5p) 两个格的长度等于 5 个板的厚度

2、joint(height)=0.75 plate(j=0.75p) 活动关节的旋转中心在板厚度的 0.75 处(旋转中心距离所在的板层的顶部是 0.25,距离板下部是 0.75)
所有钳子和圆轴组成的活动关节都具有这个性质!
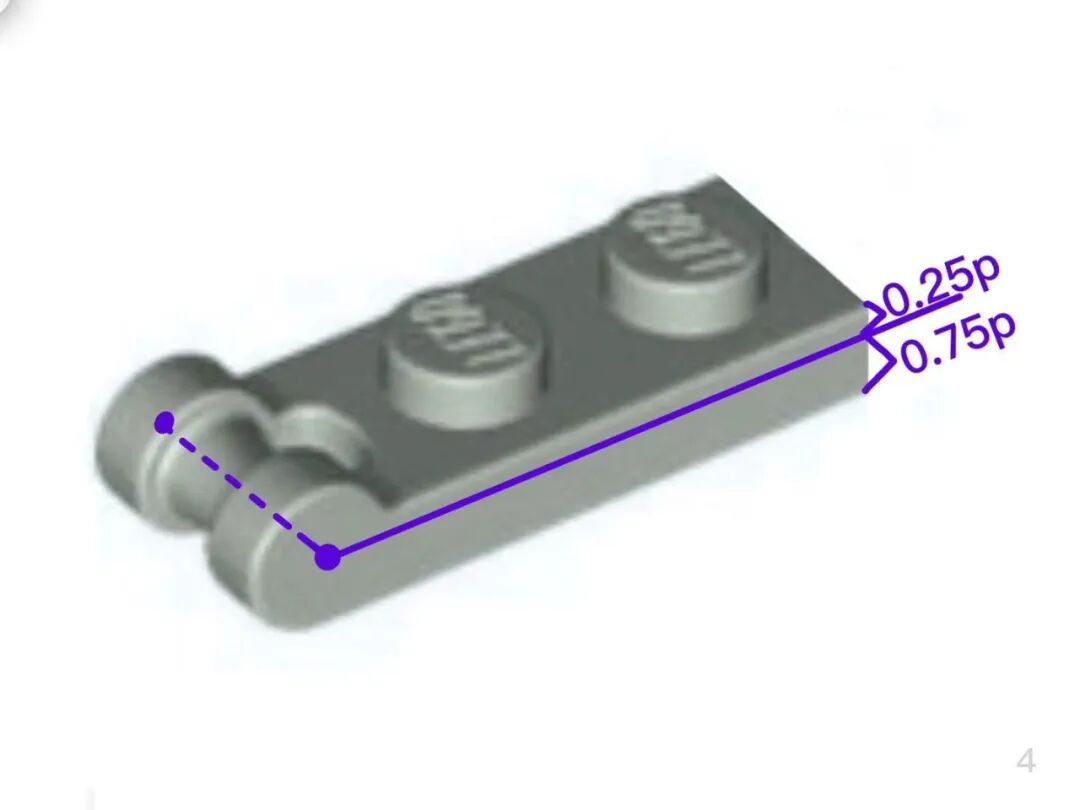
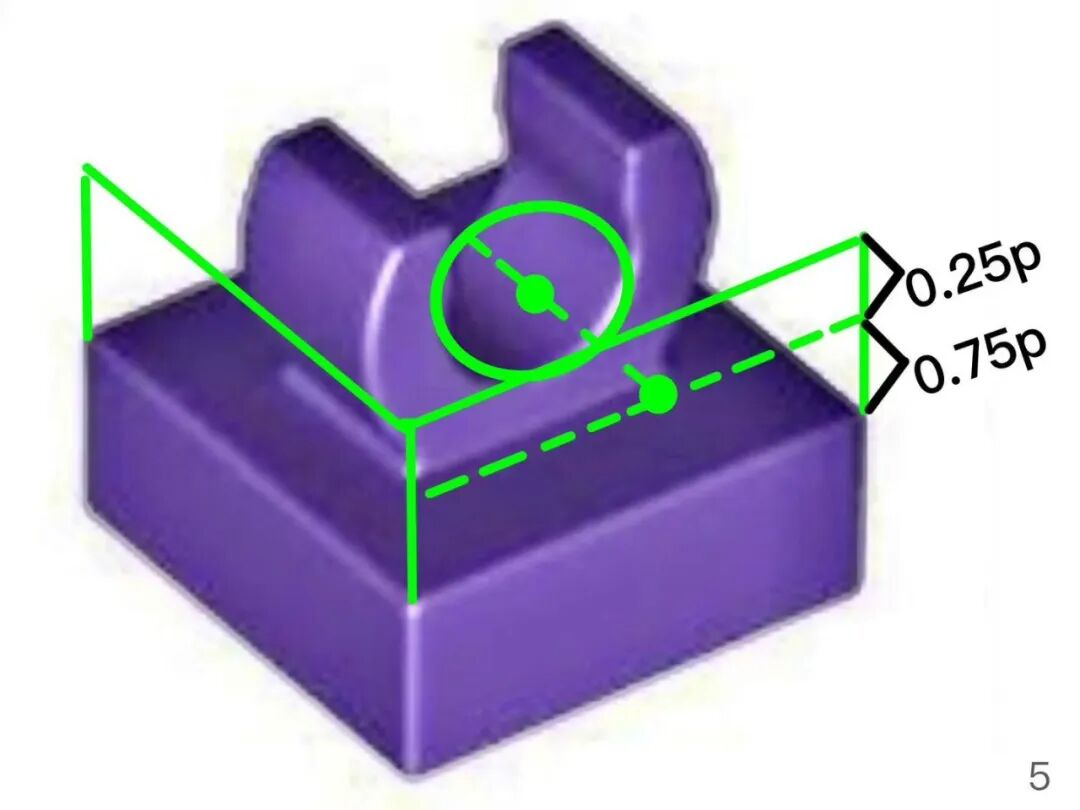
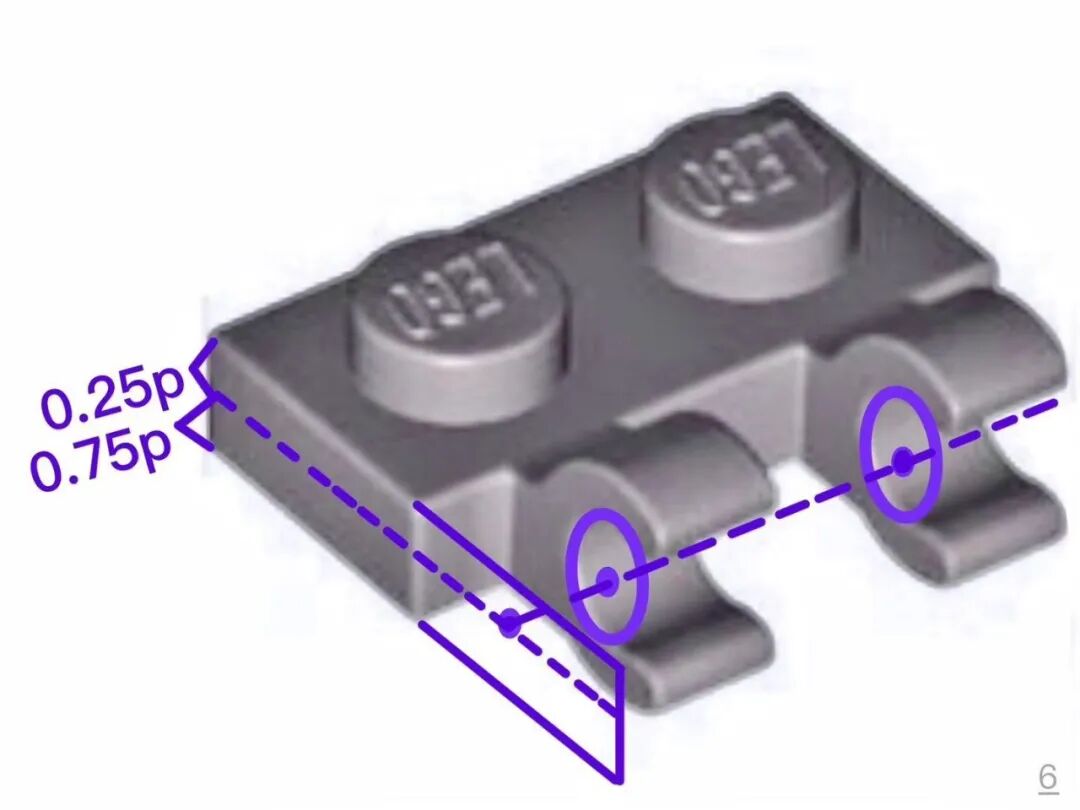

3、joint(length)=0.5stud (j=0.5s)活动关节的旋转中心在该方格的 0.5 处(旋转中心距离所在的方格的两侧都是 0.5 个单位,位于所在方格的中央)
所有钳子和圆轴组成的活动关节都具有这个性质!
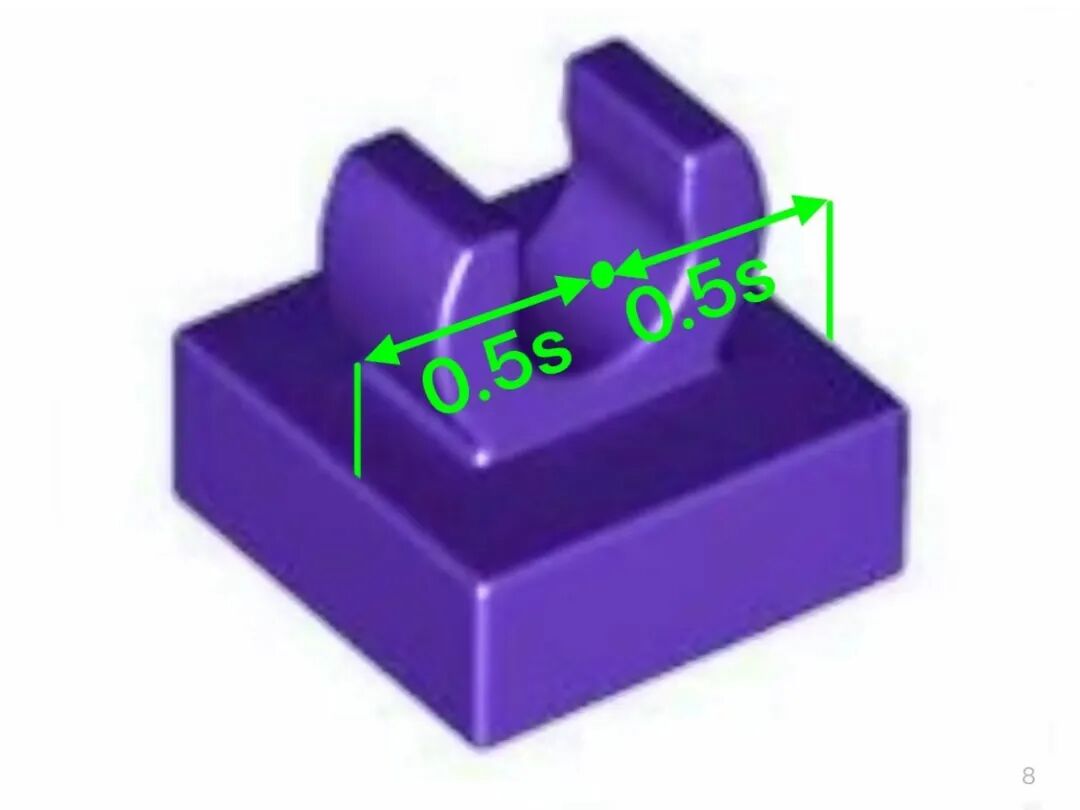
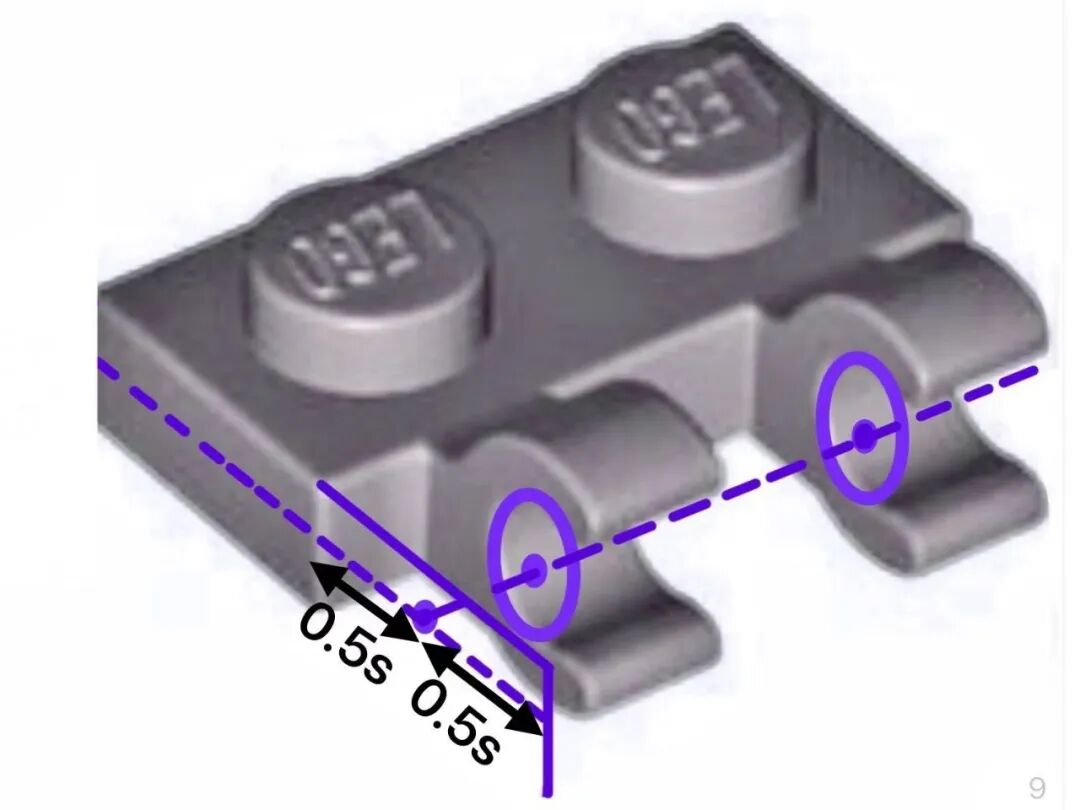
模型一

首先,我们连接 Rt 三角形斜边的两个连接轴A和B(活动关节),并作平行于零件的线段并垂直相交于一点 C 构造“直角边”。
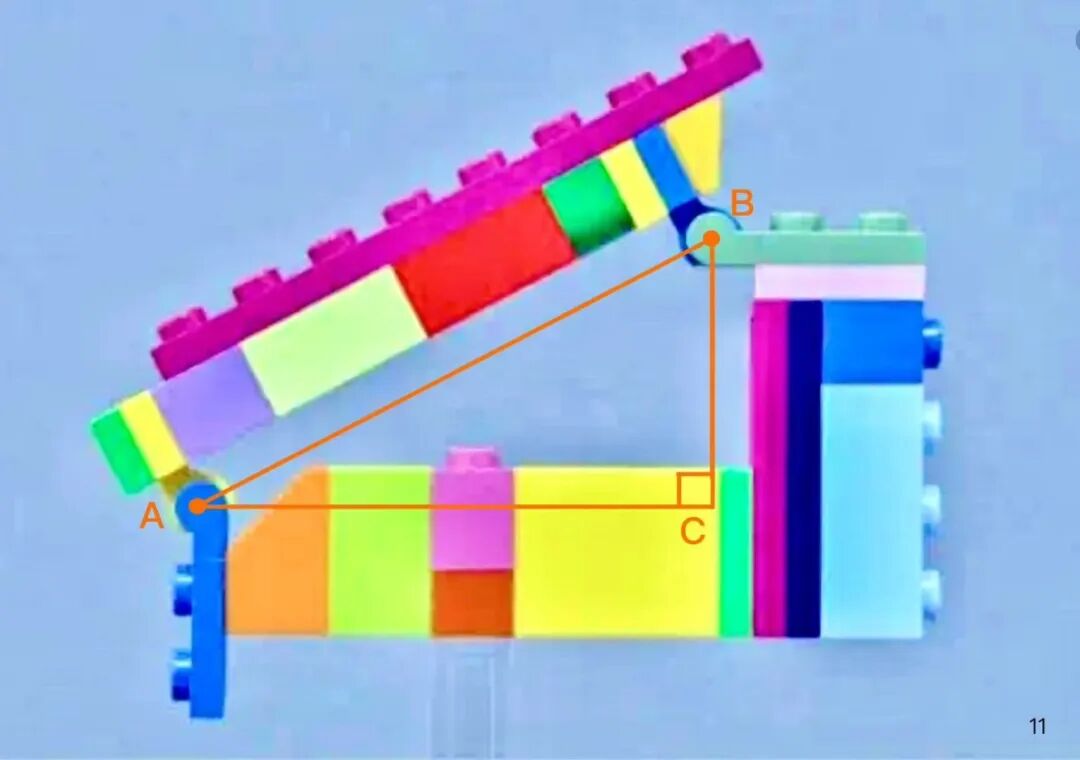
接着,我们聚焦 RT 三角形右侧的直角边 BC。
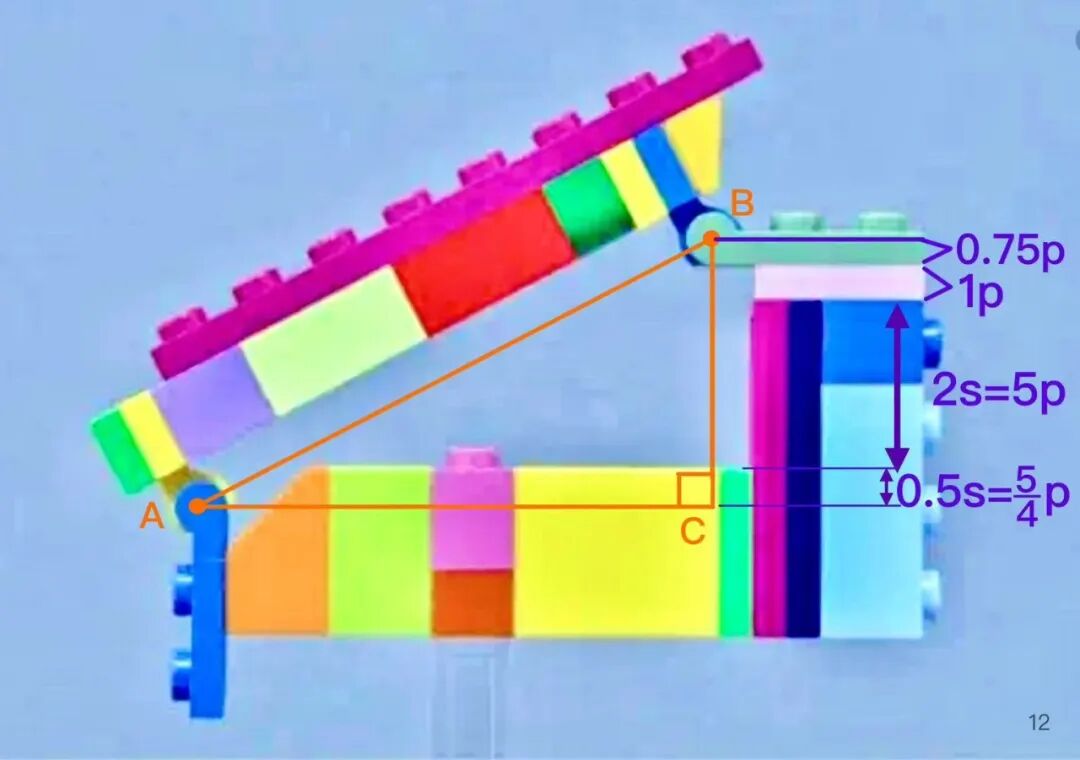
最上面的绿色活动关节在 BC 上占据 0.75p(轴 C 距离零件底部为 0.75 个板的厚度,见小公式 2)下面的粉色板的厚度是 1p。
更下方的深蓝色车灯砖和浅蓝色零件又占据了 2 个 stud 宽度,根据公式 1 把单位换算成 plate 后,它们占据 5p。
在 BC 边的最下端,则是由旋转轴 A 的深蓝色活动关节平移形成的 0.5 stud 的间隙(见小公式 3),根据 2s=5p 的公式,这个小间隙等于 5/4plate,也就是 1.25p。
现在,我们把 BC 边上的所有长度相加,0.75p+1p+5p+1.25p 正好等于 8p。
然后,我们聚焦斜边 AB。
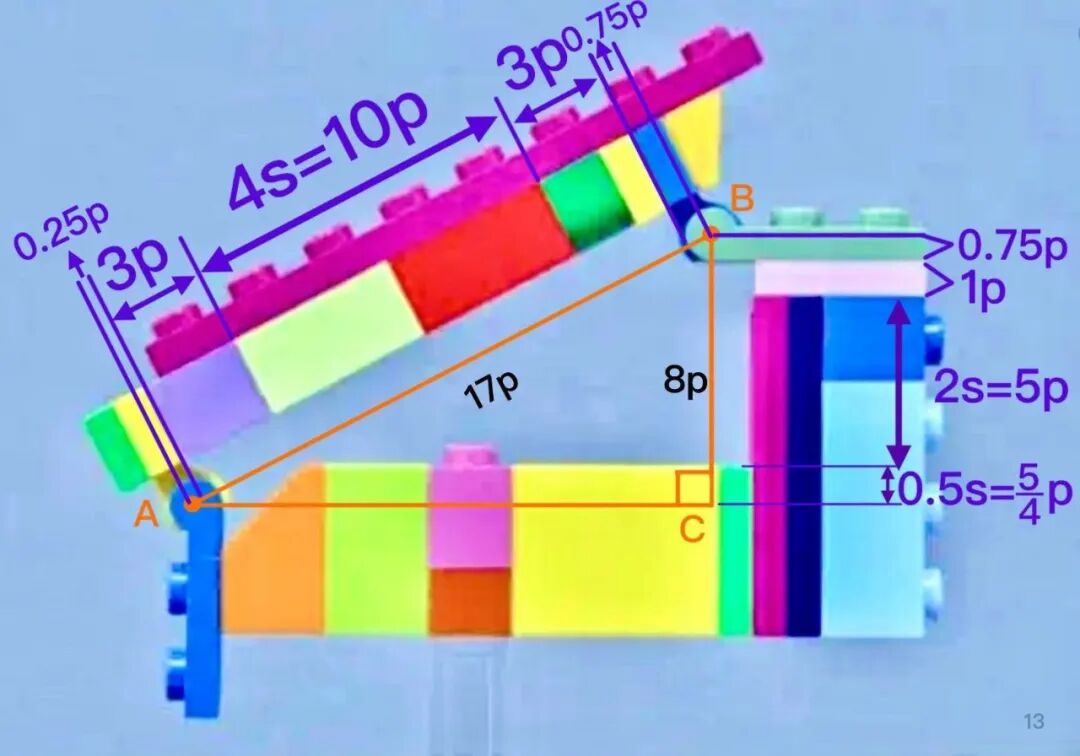
最左侧的黄色活动关节占据 0.25plate 的长度(根据公式 2),而它右侧的紫色车灯砖块的长度则是 3 个板的厚度,等于 3p。
继续向右,则是由紫色车灯砖固定的 4 个 stud 长的板,通过公式 1 换算,4s=10p,因此它的长度是 10p。
接着,一个绿色的弧形车灯砖则被用来固定粉色长板的另一头,占据 AB 的 2p,更右端的黄色 1×1plate 又拥有1p的厚度。而在 AB 的最右端,蓝色的活动关节贡献了 0.75p 的长度(见小公式 2)。
在这条边中,设计师通过粉色长板来构建飞船外壳,搭建弧形零件,而这根粉色长板却帮助我们准确地测算出了中间红绿零件对应的长度:10p。设计师正是利用 2s=5p 的性质,固定了粉色长板。
我们把斜边 AB 上的各个长度相加,0.25+3+10+2+1+0.75=17p
最后,我们来计算直角边 AC 的长度。这里是这个模型唯一的费脑筋的地方,因为这条边足足有三个搭建方向!
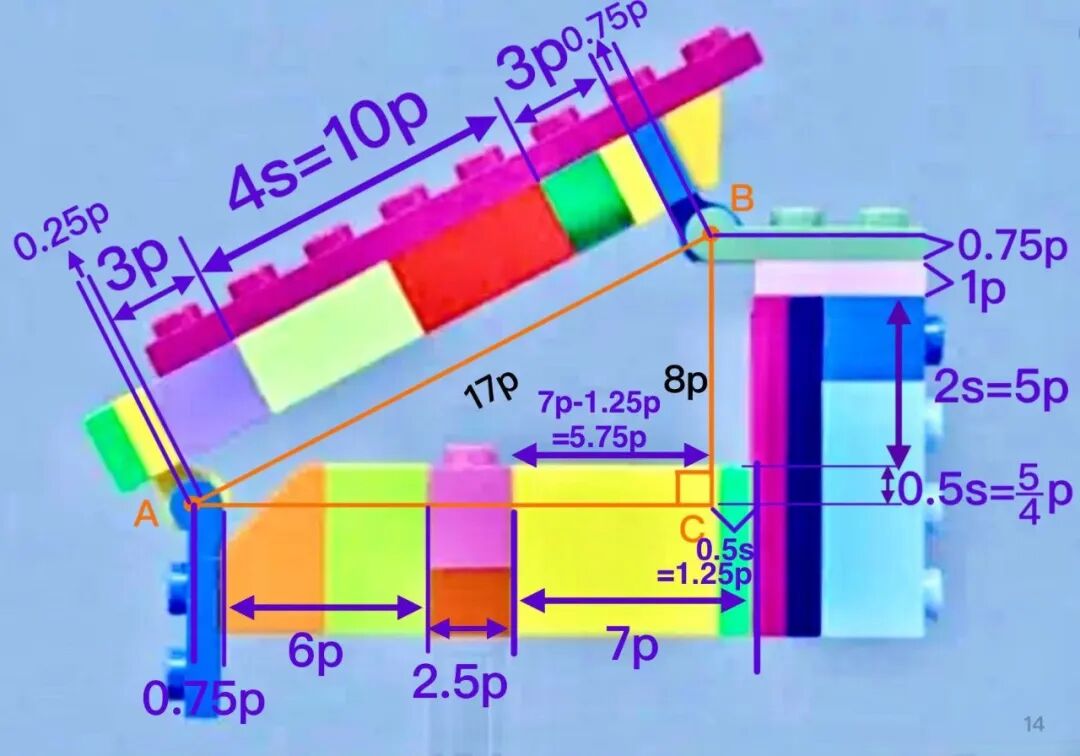
我们从 AC 的最左端开始,根据小公式 2,我们知道深蓝色的活动关节零件在 AC 边上占据 0.75p,换句话说,深蓝色活动关节在旋转轴A的右侧部分占据 0.75p。
橙色零件和绿色零件一共占据 2×3=6p。而更靠右的粉色和红色零件运用了一个经典的转向设计,中间的粉色零件其实是一块双向车灯砖,可以连接双向的零件,但它仍然是一个 stud,因此它的宽度是 1s=2.5p。
转向之后,出现了一个黄色的厚砖,它的厚度是普通砖的两倍,因此等于 6p。最右侧的绿色 plate 占 1p。
但是,我们还需要减去超过点 C 的部分,也就是超过点 B 的垂足的部分。根据小公式 3,在点 B 以右的部分的长度为 0.5stud,根据公式 1 换算成 plate,就是 1.25p。
终于,我们把 AC 上的零件长度相加,0.75+6+2.5+6+1-1.25=15p
AC=15,BC=8,AB=17,这个斜边模型正好是一个完美的直角三角形,完全合法!
模型二
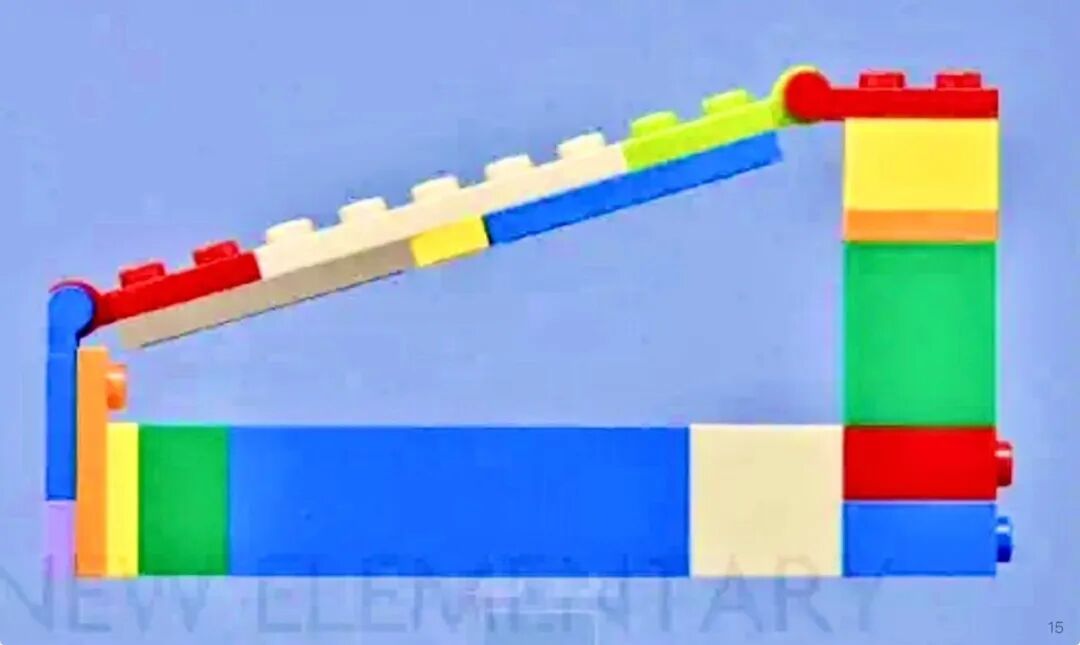
这个模型在计算方面比模型一简单许多,因为每条边都只有 1 到 2 个搭建方向!
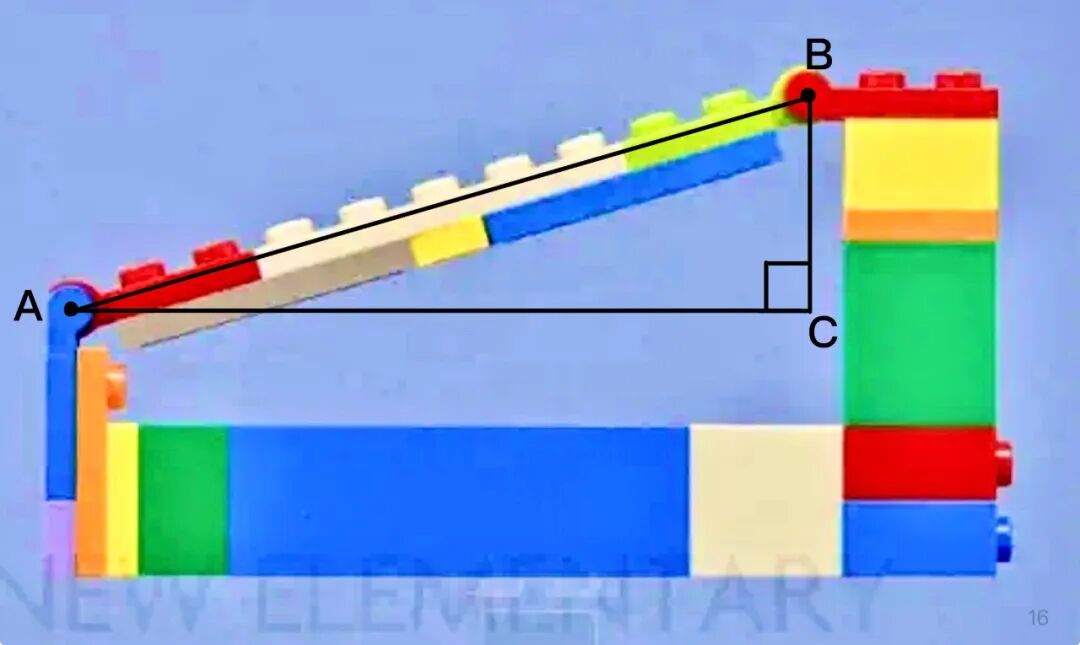
首先,我们计算斜边 AB。
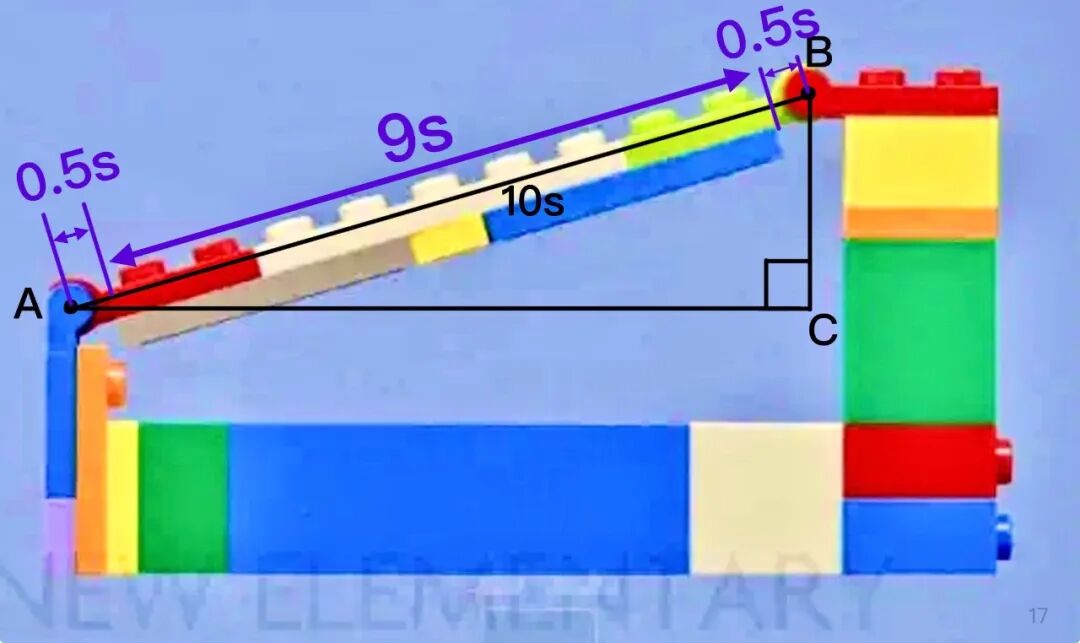
这个模型较大,所以我选用了 stud 作为单位。
横梁:9s
活动关节:0.5s+0.5s(根据公式3)
总长度:9+0.5+0.5=10s
然后,我们聚焦直角边 BC。
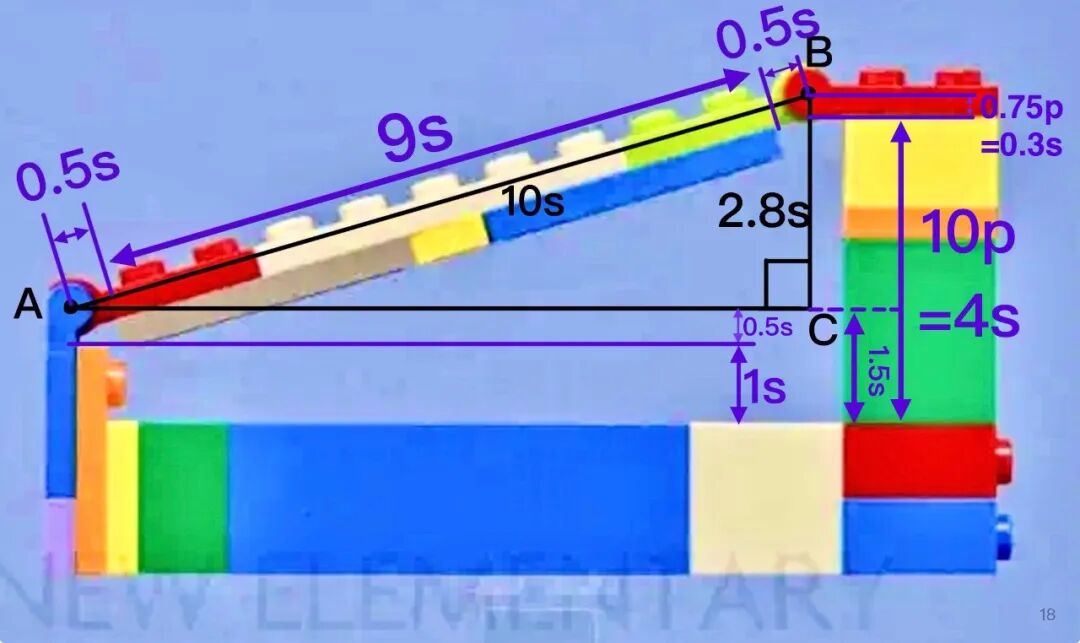
我们以从上到下的顺序计算长度。
红色活动关节:0.75p=0.3s(根据公式 2 和公式 1 的变形 1p=0.4s)
黄砖+橙色板+绿色厚砖:3p+1p+6p=10p=4s(根据公式 1)
接着,我们需要减去超过点 C 的部分(点 C 以下的部分)。
A 点处的蓝色活动关节:0.5s(公式 3)
下方的橙色零件:占据 1s
总长度:0.3+4-0.5-1=2.8s
最后,计算直角边 AC 长度。
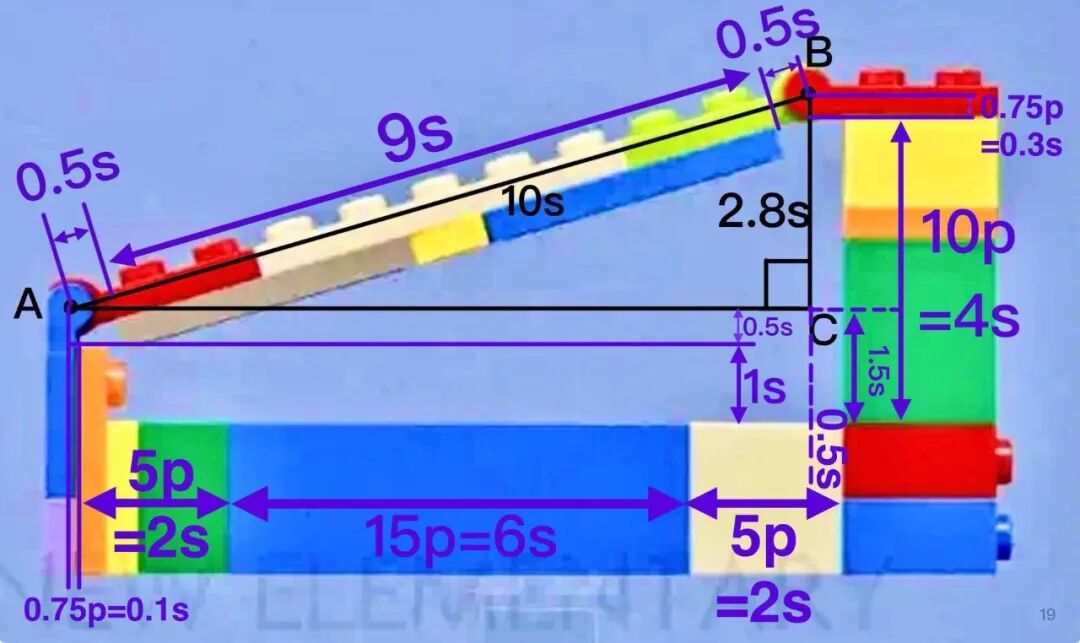
我们以从左往右的顺序计算长度。
蓝色活动关节:0.25p=0.1s(根据公式 2 和公式 1 的变形 1p=0.4s)
橙板+黄板+绿色砖:5p=2s(根据小公式 1)
蓝色超厚砖:15p=6s
浅棕色砖:5p=2s
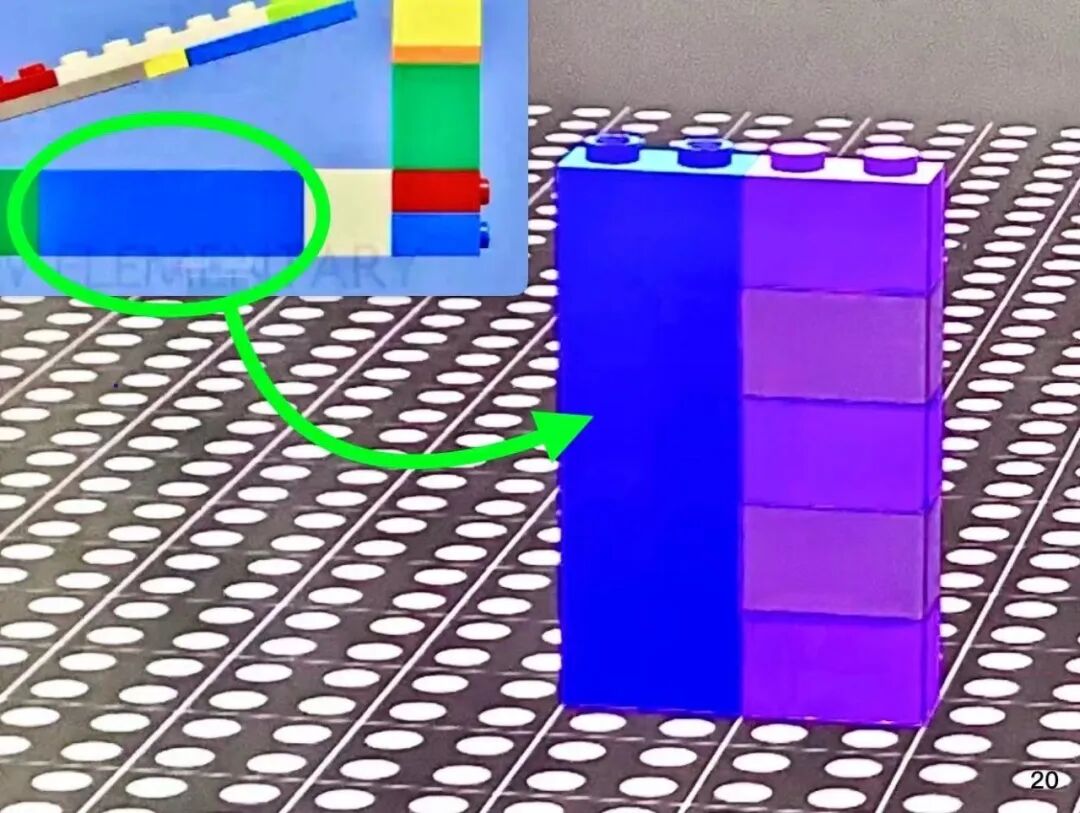
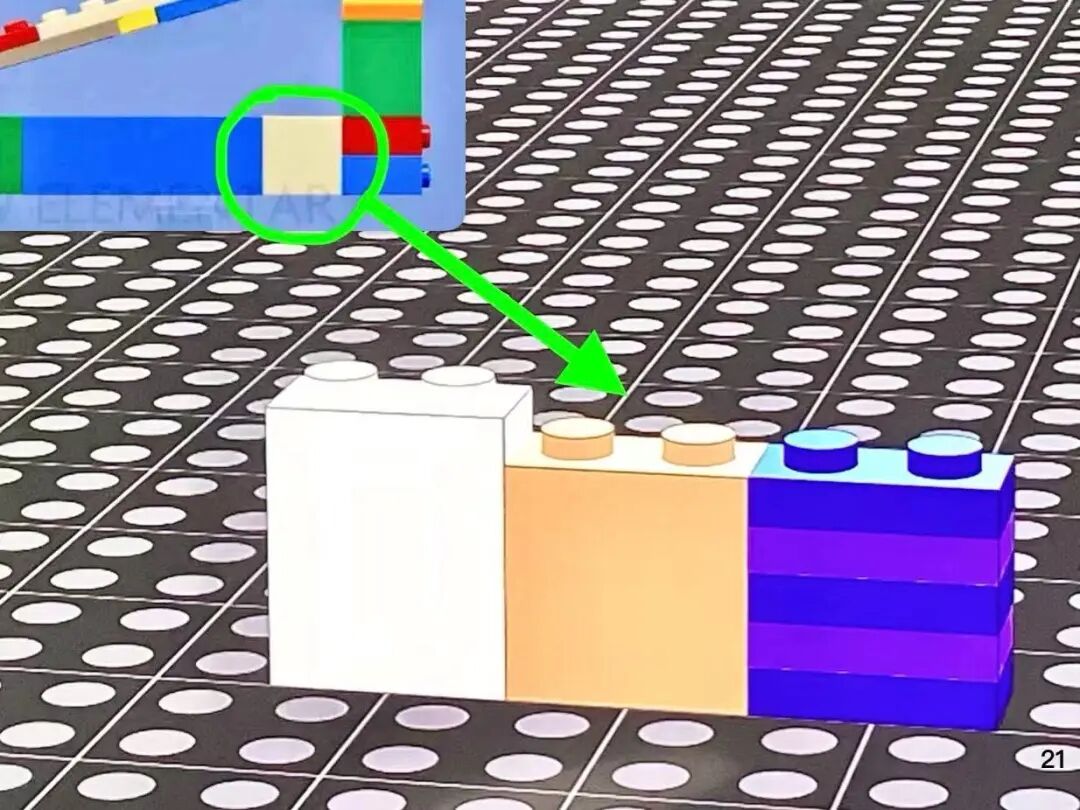
接着,我们需要减去超过点 C 的部分(点 C 以右的部分)。
上方 B 点的活动关节间隙平移下来:0.5s
终于,我们把所有长度相加再减去超出部分。0.1+2+6+2-0.5=9.6s
AC=9.6,BC=2.8,根据勾股定理 9.6平方+2.8 平方=100=10 平方斜边长度正好是 10,完全合法!
总结一下这两个结构消除 0.75p 和 0.25p 的活动关节间距的方法:
通过两个活动关节的同方向摆放(见模型一的斜边 AB!)消除 0.75 和 0.25。
利用活动关节的性质(公式 3) 0.5s=1.25p 的间隙,填补含有 0.75 的边使其变成整数,或减去边中的 0.25 是其变成整数。(见模型一的 C 点)
矩形转换法模型
计算完这两种砖块勾股结构,我们再看看第三种斜面结构:矩形转换法。也就是 Rectangular Transformation 技巧,简称 RT 技巧。
这种搭建方法巧妙地利用了图形在旋转后不会发生形状变化的常识,将矩形的一部分进行了方向对调。而这个 RT 模型的原型是一个矩形,因此我把它进行了复原。
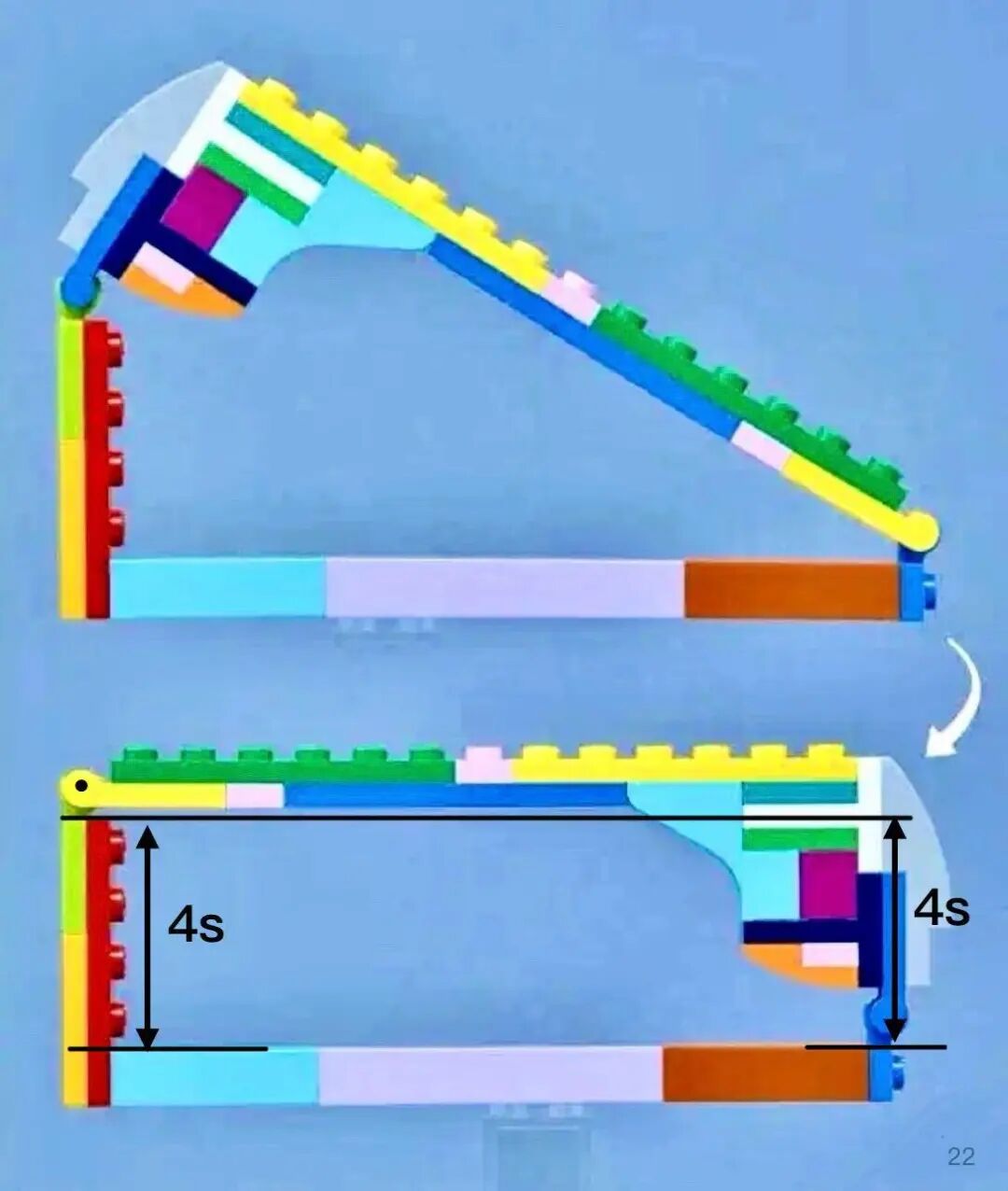
两条较短的对边的主体框架都是 4 个 stud,但它们上方的缝隙却十分复杂,因此我作了 a,b,c 三条直线以便计算。
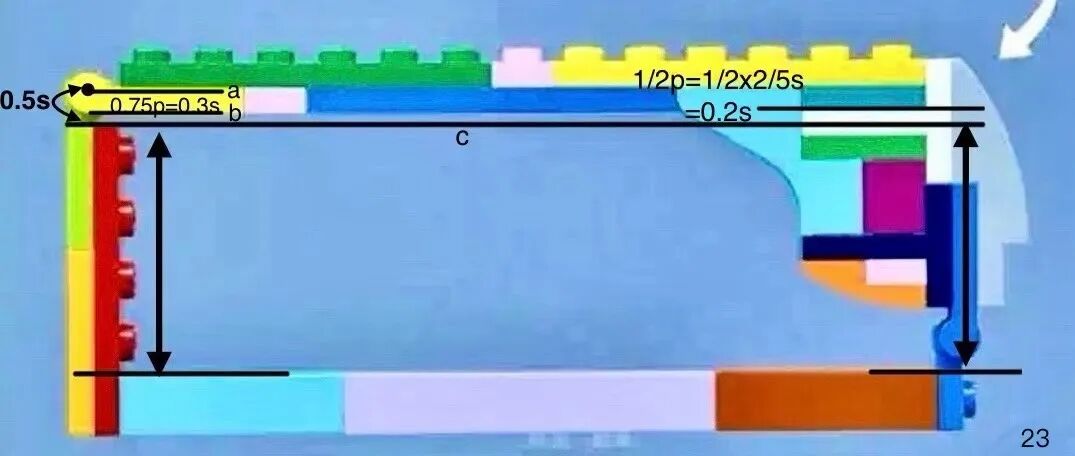
直线 a,c 之间的距离是 0.5s(根据公式 3)而 a 和 b 之间的距离是 0.75p,根据公式 1(2s=5p,p=0.4s)可换算成 0.3s。所以 a 与 c 之间的距离就是 0.5-0.3=0.2s,换句话说,上层框架与左侧框架之间的距离是 0.2s。
再来看右侧框架,右侧框架与上层框架之间的间隙是白色 T 字件的一半,也就是板厚度的一半,1/2p。根据公式 1(2s=5p,p=0.4s),它的间距等于 0.2s。因此,左侧框架与右侧框架距离上层框架都是 0.2s。所以这个 RT 模型也完全合法!
可以看出,复原后的封闭图形是一个完美的矩形,两组对边都分别相等,因此这个结构仍然合法!
设计自己的勾股结构
计算完这三种斜面拼搭结构,CTR 常子发现砖块勾股结构的模型都存在一个小缺陷:搭建方向太多,导致很难做到斜面结构与飞船主体框架的全方位固定。于是,他也自己设计了一款砖块勾股结构。下面是 CTR 常子第一人称的设计教程。
首先我决定使用 6,8,10 的勾股三元组。因此,AB 间的距离是 10。
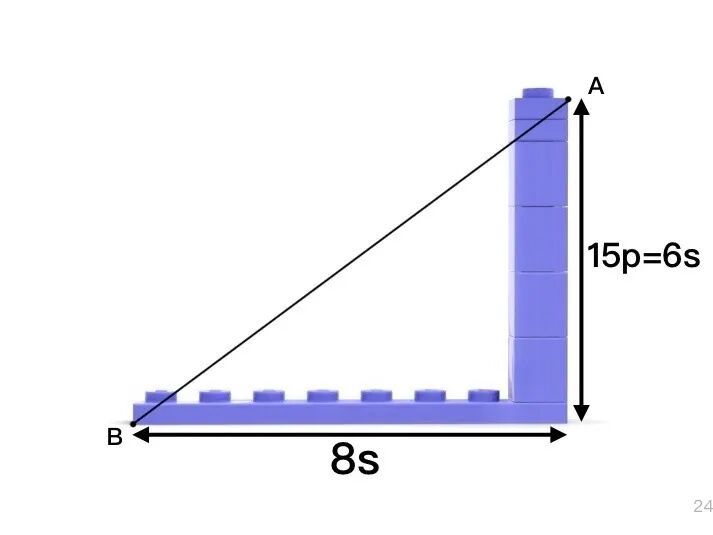
然后,我把一个活动关节放在了三角形上。此时,原来的顶点 A 不再是三角形顶点,而新的顶点则是旋转轴。旋转轴与原先顶点A的横向距离为 1.5s,纵向距离为 0.75p。
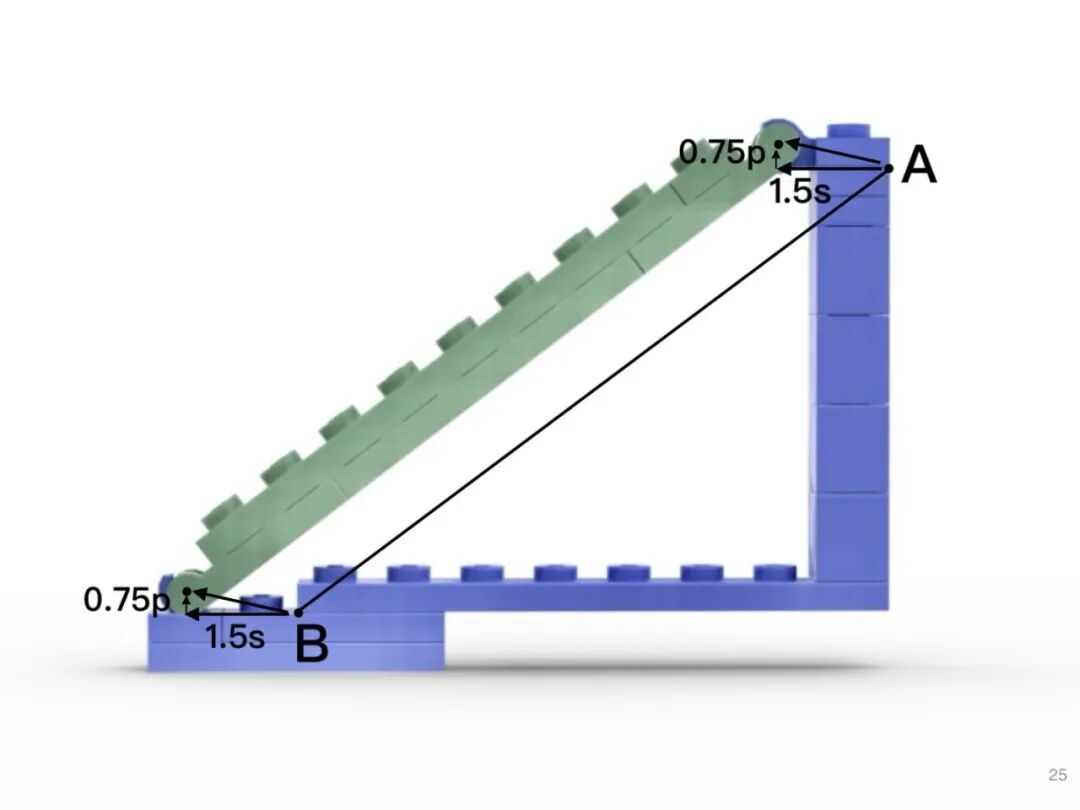
因此,原先的顶点 B 也将不再是顶点,而新的顶点距离B的横向距离一定也是 1.5s,纵向距离一定是 0.75p。
考虑到很多 MOC 需要小型比例的斜面,我又做了一个 3,4,5 的直角三角形。
首先,我构建了框架。它仍然以 s 为单位,一条边是 4s,另一条边是 7.5p=3s(我巧妙地利用了侧面零件的 0.5p)

这次,顶点横向变化距离是 1.5s,纵向距离是 0.75p。这样,一个绝对合法的坚固的 3,4,5 直角三角形斜面结构就做好了。
我总结出了一些构造砖块勾股结构的方法供大家搭建时参考。
1、先用砖和板构造直角边,如果遇到 2s=5p 产生的小数,可以把它扩大(如 3,4,5 变成 6,8,10)同时也可以像我一样,使用侧面零件构建小数。

2、在用活动关节链接斜边时,先观察横向变化距离和纵向变化距离,保持两个顶点的变化距离相等。
END
希望这篇文章能帮助你构造坚固合法的勾股结构!
如果你想要构造砖块勾股结构但又没有把握,欢迎随时在评论区里咨询,CTR 常子会在第一时间向你制作符合要求的斜面。
如果你设计出了其他砖块勾股结构(比如 8,15,17 的斜面),欢迎在评论区分享,CTR 常子会在第一时间把你设计的结构发表在新的文章里。
本文为酷玩潮读者 CTR 常子投稿












评论留言