作者:Arno Knobbe 编译:酷玩潮
hello 大家好!
今天将是一场超费脑的数学与乐高积木的较量,如果你是逻辑和数学苦手,现在退出还来得及!警告!

今天我们和 Arno Knobbe 来聊另一个在乐高拼搭中非常实用的技巧:反向楔形件(reflected wedges)。
首先,我们需要了解一个技术:糖网格(Sugar Grid):在乐高积木原本的直角网格系统之外,利用一定规律的“斜向连接点”来实现稳定的倾斜结构布局。
好了,go go go!
反向楔形件(Reflected wedges)
说得简单点,一对反向楔形件就是两个形状相同但互为镜像的乐高楔形零件(可能是砖或板),它们的斜边拼合在一起:

你也许注意到了:楔形的斜边通常不是整数长度(有些甚至是无理数),所以在乐高楔形件系列以外很难找到能顺利对齐的零件。
反向楔形件的妙处就在于,用两个镜像件就能让这些“难对齐”的边无缝贴合!
乍一看,矩形拼角法和反向楔形件这两种方法像是完全不搭界,但实际上,它们是同一件事的两种表现方式:

这两个楔形(三角形)其实就是那两个矩形结构中一分为二的部分。
它们的对接边,就是让红色和白色矩形倾斜对齐的那条斜向对角线。
反向楔形件非常适合将整块组件以特定角度连接到主结构上。
这个方法可以不断重复使用,从而形成更大的乐高楔形结构,比如下图所示:
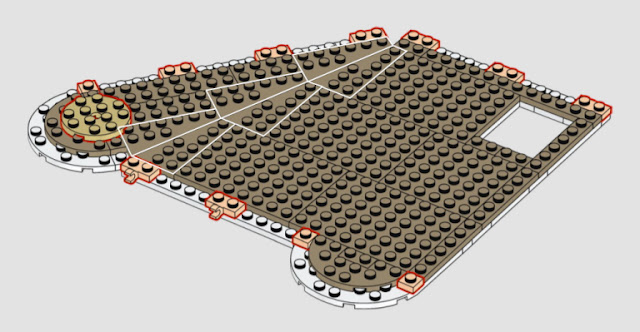
如图所示, 10297 精品酒店的一层平面图:酒店左侧的整块区域(不仅是这一层)都以 36.9° 的角度建造,具体方式是将三块楔形件与三块镜像楔形件拼在一起。
那这些板子是怎么固定的呢?

最直接的方法当然是用乐高零件中的铰链板(hinge plates)或铰链砖(hinge bricks),可以放在楔形件的上方或下方。
你不一定非得用我图上那种三铰链组合,但如果你要用铰链,一定要把铰链的旋转轴对准乐高网格的交点,像图中这样。
铰链一定是唯一的选择吗?
在糖网格流行的今天,铰链板不一定是最佳解了。
实际上,你可以用糖网格的定位凸点直接固定楔形件——前提是楔形件够大,能覆盖住足够多的凸点。

糖网格有不同的比例,这里这个网格是 1:2 比例(每个蓝点之间,水平移动 1 模块,垂直移动 2 模块)。
而图中的两块反向楔形件恰好也是 1:2 比例。
什么是 1:2 楔形件?

这个比例的意思是:对角边从一个角到另一个角时,水平跨 1 模块,垂直跨 2 模块。
上图展示了多种 1:2 楔形件,甚至还包括弯曲款。
虽然这些楔形形状不一,但角度完全一致,所以都可以互相拼合。图中的蓝点和白点就是糖网格上的连接定位点。
双重网格(The dual grid)
我们回过头再看看糖网格,特别是刚刚提到的 1:2 糖网格:

糖网格的比例很容易通过蓝色凸点的分布看出来:横向 1,纵向 2。
但仔细看那两个颜色更深的凸点,它们之间是横向 1,纵向 3!
什么鬼?一个网格怎么会有两个比例?
其实这是糖网格的隐藏机制:每个糖网格都有主比例和对偶比例。在这个例子中,主比例是 1:2,而对偶比例就是 1:3。
这意味着,每一个糖网格都支持两个斜向角度(除了原有的 0°正交网格)。
你其实已经见过这两个角度了。下面这个例子用 1:2 糖网格支撑一个 4 × 4 的正方形:

蓝色和白色砖之间的角度是 53.1°(= 2 × arctan(1/2)),蓝色和红色砖之间的角度是 36.9°(= 2 × arctan(1/3))。两者加起来正好 90°。
所以 1:2 糖网格也支持 1:3 的楔形
虽然看起来简单,实际上要在糖网格上正确放置 1:3 楔形并不容易。
你需要精准地对齐角落。这时,白色的偏移凸点可以派上用场。
虽然它们容易“撞”到楔形边缘,但它们是你放楔形角落的参考标记!

图中红色凸点就是标记楔形角落的位置。放置前可用作参考,放上楔形件时需将其移除,以免干扰贴合。
干净连接:反向楔形件的最大魅力
反向楔形件可以帮助你把乐高中的斜结构和主网格之间的连接做得又稳又干净,几乎没有空隙、没有强扭感。
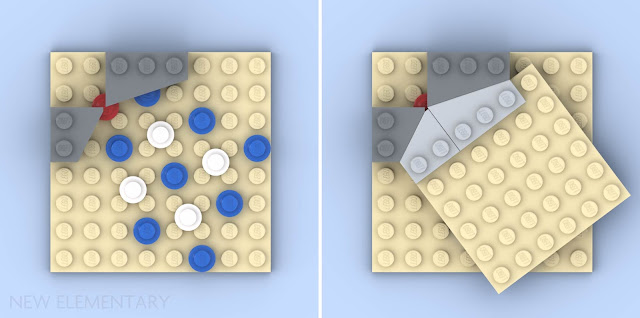
上图是一个干净拼接的乐高 6 × 6 板,两个方向上都采用了角度接口。你有没有觉得这结构很眼熟?

没错!这几乎就是乐高套装 10305 雄狮骑士的城堡中的一个设计,只不过它还用的是中世纪铰链——糖网格还没影呢!
构建 45° 的方法?
既然 1:2 + 1:3 可以拼出 90°,那是不是一个 1:2 和一个 1:3 拼在一起就是 45° 呢?
答案是:是的!你得相信 Arno Knobbe,她说这在数学上是完全可行的。

Arno Knobbe 这里用了一个非常实用的零件:A 字板(15706),来把两个楔形件固定在 45°。
目前糖网格还没法直接支持 45°,所以只能靠这种“硬件拼接”。
另一种方式是使用“膝关节”件:

但拼着拼着就对不上了……
虽然 1:2 + 1:3 的组合角度很优雅,但会出现一个问题:两个端点不一定能对得上,这是因为它们的斜边分别是 √5 和 √10,两者差了个 √2 倍,数学上不兼容。
不过,加拿大乐高拼搭大神 Joel Short 找到了办法:

他采用了“交错拼法”:1:2 + 1:3 + 1:2 + 1:3 ……这样在视觉上能让两端接近对齐。
虽然其中一块楔形有点“卡进”了另一块,但从效果上来说,这几乎就是拼成功了。
更多比例组合
我们再来看几个冷门乐高拼搭比例。
1:4 和 1:6 的楔形件很常见,比如下图:

按照上面提到的公式:
对偶比 = (m – n):(m + n)
你会发现:
- 1:2 的对偶比是 1:3 ✅
- 1:4 → 对偶比是 3:5
- 1:6 → 对偶比是 5:7
不幸的是,乐高集团目前还没有这些奇特对偶比例的标准楔形板。
(乐高官方,如果你在看,求你做一个!)
不过,并不是只有楔形件能搞定斜角——奶酪砖(54200)的斜边就是 3:5!

图中右侧是用 1 × 1 奶酪砖侧贴拼出的 3:5 比例结构,可以和 1:4 楔形板拼在一起。
进入极客级别的拼法
下图展示了两个极为罕见的角度配对组合:

- 前排是 22391(4 × 4 尖楔,2:3)+ 30382(2 × 16 三楔,1:5)
- 后排是 30036(中心格栅,2:5)+ 3933/3934(小翼片,3:7)
- 连接结构使用的是 A-frame 框架。
MOC 实例:飞船拼装
前面提到的黑色楔形,是最难用进作品里的组合。
但乐高 MOCer Tom Loftus 恰好用这个组合设计了一艘超炫的未来星舰!

厉害吧!
总结一下:
反向楔形件,不只是个拼角度的小技巧,而是你在乐高拼搭中实现“非对齐结构”的关键利器!
它能让你自由切换角度、干净连接斜结构,和糖网格结合后,更是能帮你构建复杂又稳定的结构。
如果你已经玩腻了直来直去的拼搭逻辑,是时候试试逃离正交网格了!
*资料来源:newelementary












评论留言