隐身的数学—那些隐藏在乐高积木背后的数学奥秘
今天你将面对的是一道拔高题，对于所有moc玩家来说，这篇内容也许会挑战你的全部数学知识贮备，但请相信我，读物之后对你会有很大启发的。
首先问几个问题，你在平时拼乐高的时候是否看到了蕴藏在里面的数学奥秘？以及数学是如何运用在乐高当中，进行一次完美的搭建？
为了帮助回答这些问题，我们很高兴编译这篇来自bricknerd的Deep Shen的客座文章，讨论那些隐藏的乐高当中的数学谜题。
隐藏的数学谜题
每次当我搭建官方套装的时候，我都感觉这是一个让我身心非常愉悦的过程，我相信，所有的AFOL也大多会有这样的感觉。当我们打开包装盒，排列所有编号的零件包，然后根据说明书开始将所有搭建好的成品放在一起的时候，总是令人感到兴奋。但是久而久之，我们会遇到一种让我们感到困惑的问题，总是让我们想去了解和挖掘：“这些设计师是怎么知道应该这样去搭建的？”
可以肯定的是，答案就潜伏在所有乐高积木背后隐藏的数学奥秘中。当我们搭建一些建筑物的时候，将乐高零件置在规则方形网格的范围之外，以创建有角度的墙壁或者圆形。在这个过程当中，我们就会遇到很多关于数学的问题。
但是如果数学是乐高搭建过程中不可或缺的一部分，这是否意味着乐高设计师需要随时准备好计算器或白板来计算数字？
然而并不是，乐高搭建的美妙之处在于，有无数种不同的方式将各个部分组合在一起。如果您能花足够的时间玩乐高，那么您一定会发现一些新的有趣的技术，而并不总是了解底层的数学逻辑。
有时我想知道新的套装中的出色连接是由数字计划出来的，还是只是设计过程中的发生的偶然事件。不管是什么原因，作为一个技术控，我对官方套装中使用的一些巧妙技术，进行逆向工程以试图揭示使它们起作用的数学逻辑，是非常令人着迷的。
注：今天的文章可能有些枯燥，各位看官，请耐心看完，小编我尽量将这些枯燥的数学原理，说得有趣一点。
用到勾股定理的斜面墙壁
让我们从街景系列——10297精品酒店开始说起。它于2022年1月1日发布。看到这个套装的第一感觉，就是让小编注意到，这座街景建筑，它的斜角设计，并不是寻常的三角形形状。
众所周知，乐高是基于规则的方形网格进行搭建的，那么它们是如何做出这个形状的，我们能弄清楚它背后的数学原理吗？
如果我们经常搭建乐高，就会发现，将乐高积木放在相对于乐高平面网格0/90/270/360度以外的任何角度方向，都很难确保将砖或板两端的颗粒对齐。
乐高网格上的颗粒，仅在得到的直角三角形满足勾股定理 (a²+b²=c²) 时才有效。最小的勾股定理是 (3,4,5)，这就是精品酒店里使用的基础数学。但它使用勾股定理表现的方式并不明显。实际上，如果您查看此建筑中的斜面墙壁，您可以数出六个独立的 (3,4,5) 三角形，甚至包括两个彼此相交的三角形（下图三角形序号4和6）。
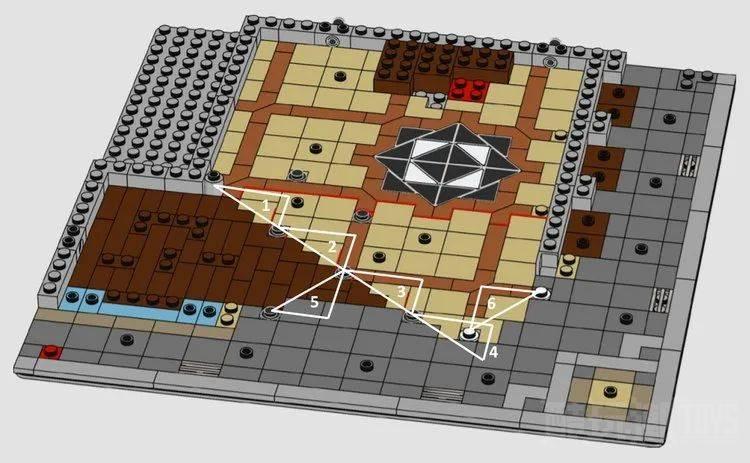
鉴于三角形1-4的斜边（最长边）是用长板连接在一起的一条直线，我们甚至不需要连接三角形 1 和 4 的外端。三角形 5 和 6 的斜边位于与连接三角形 1-4 的斜边成直角的直线上。
镜像斜边搭建技巧
当我们分析精品酒店这栋建筑的时候，分隔建筑物三层的地板部分和屋顶部分是使用普通板和楔形板建造的，并且不知何故，它们的倾斜侧面与建筑物的倾斜墙壁能够完美对齐。难道这都是巧合？小编发现并不是。我们需要进入一些基本的三角几何数学来解释这一点。
在直角三角形中，对于任何一个较小的角，与角相对的边与相邻边的长度之比称为切线。无论三角形的大小如何，这个比率对于给定的角度都是固定的。如果我们已经知道比率，我们可以使用正切函数的倒数或反正切函数（在大多数科学计算器中可用）来计算角度。在 (3,4,5) 三角形中，最小角的切线为 3/4 = 0.75，其反正切值为 36.8 度。
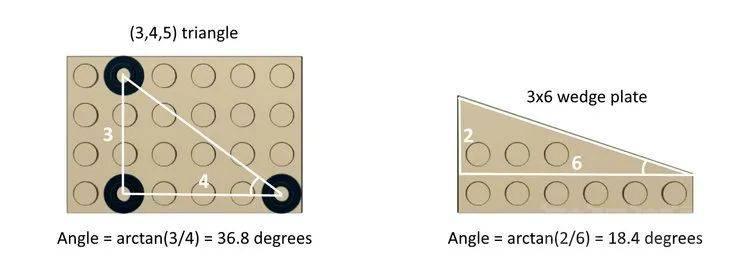
如果您查看精品酒店的地板部分或屋顶部分，您会发现他们使用两个镜像的 6×3 楔形板来创建倾斜的一面。每个楔形板都有一个直角三角形，其切线为 2/6 = 0.333，其反正切值为 18.4 度。因此，这些楔形板中的两个将给我们一个 36.8 度的组合角度，与我们在倾斜墙上的角度相匹配，这是有道理的。
我们可以使用公式来计算给定角度两倍的正切来确认这一点。
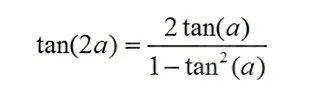
代入数字，我们看到由楔形板产生的角度的两倍的正切为 (2 x 1/3) / (1 – 1/9) = 2/3 x 9/8 = 3/4，这与由 (3,4,5) 勾股定理创建的角度的正好吻合。这样搭建，就让作品看起来很整洁，是不是？
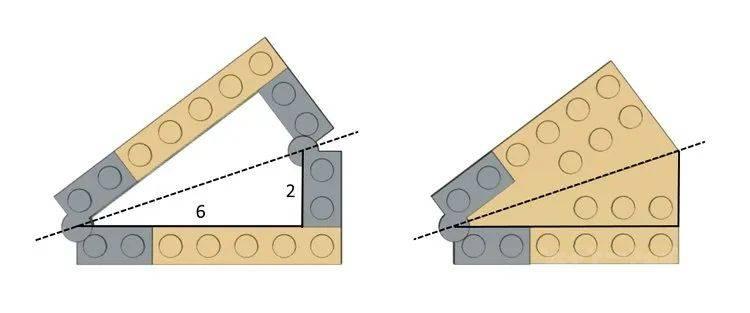
此处使用楔形板的方式是“镜像斜边”技术的常见应用。这绕过了这样一个事实，即对于任意直角三角形，斜边的长度并不总是整数。由 6×3 楔形板创建的三角形的斜边是 √(6² + 2²) = 6.32 个颗粒。即使我们不能沿斜边放置乐高元素，我们也可以通过沿斜边直角三角形并将乐高零件沿第二个三角形的其他两侧放置来创建倾斜的墙。这两个三角形必须使用铰链板固定在一起，这正是10297精品酒店套装中所做的。
使用转盘进行斜墙的搭建
有角度的墙也可以用转盘建造，你可以在多个官方套装中看到这一点。让我们以80107新春灯会为例，其中使用 4×4 转盘将拱形人行天桥以一定角度连接在锦鲤池上方。
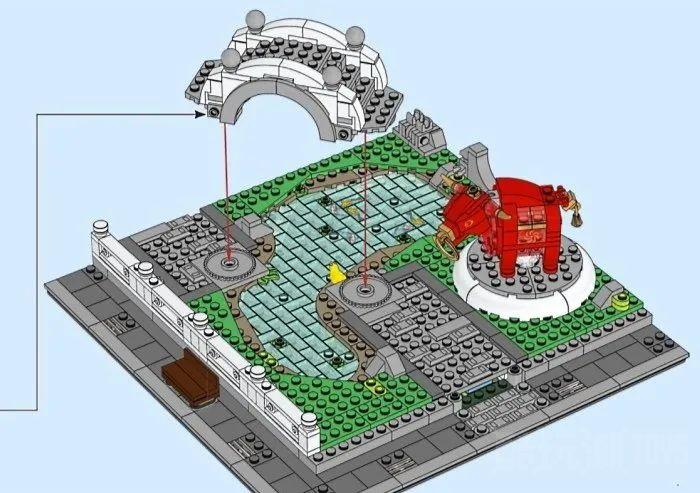乐高转盘由一个可以像普通板件一样安装的底座（2×2 或 4×4）和一个可以 360 度自由旋转的顶部组成。2×2 底座需要匹配的顶部元件，而 4×4 底座可以容纳各种乐高零件，包括 4×4 圆板。
即使我们使用转盘来创建倾斜的墙（或以一定角度连接的结构，如下图所示），我们本质上是在创建满足勾股定理的直角三角形。这个三角形的边与转盘上的旋转轴（顶板的中心点）相交。本例中使用的勾股定理三元组是 (6,8,10)。
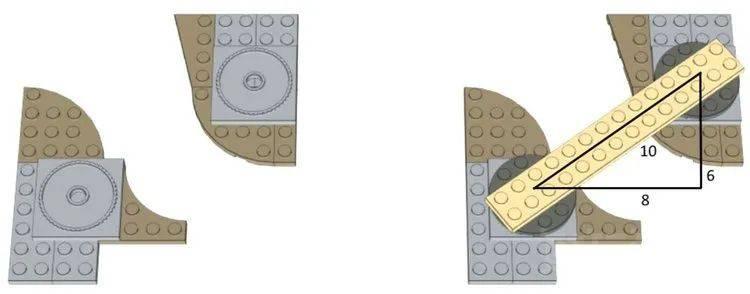
使用“三倍数”的斜墙
正如我们所看到的，如果我们只限于勾股定理三元组，我们就没有更多的选择。勾股定理的大多数应用都使用最小和最常见的三元组（3,4,5），如精品酒店套装或新春灯会中的倍数（6,8,10）。
但是在某些情况下，可以稍微逃脱严格勾股定理三元组，但对于实际目的来说足够接近的三元组（三个数字的倍数）。我喜欢称这些为“三倍数”。
当我们使用“三倍数”创建有角度的墙壁时，使用像铰链这样自然有一点摆动空间的零件，总会有出人意料的效果。这可以最大限度地减少您在连接有角度的部分时对乐高元件施加的压力。
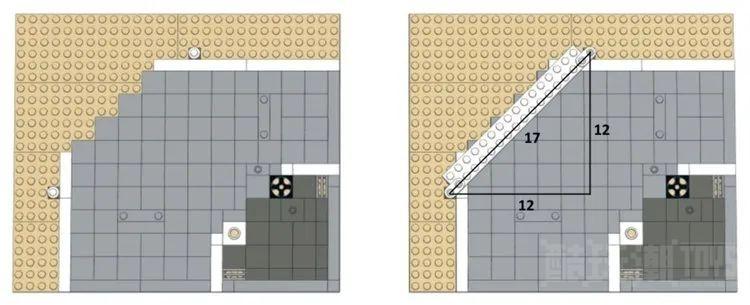
我经常在我的构建中使用像 (5,5,7) 和 (7,7,10) 这样的“近三倍”，其中一些具有额外的优势，允许我们以 45 度角创建墙壁（这不是毕达哥拉斯三元组可能）。在查看乐高于2019年初发布的10264街角汽车维修站的说明之前，我不知道有任何官方套装使用了“三倍数” 。
这个套装的一个很明显的地方是车库前立面的很大一部分是以 45 度角建造的。加油站上方还有一个遮阳篷，该遮阳篷垂直于该立面（最终与底座成 45 度角）。
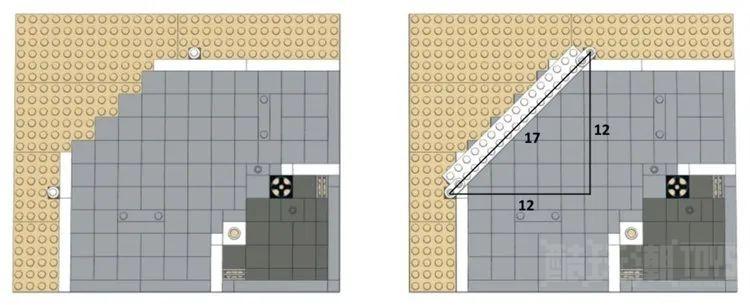
如果我们深入研究这个套装的说明书，我们会看到倾斜部分是建立在一个 2×16 板上的，该板使用 1×2 圆板以 45 度角连接。倾斜部分的总长度为 17 个颗粒，在两个连接点的颗粒之间进行测量。
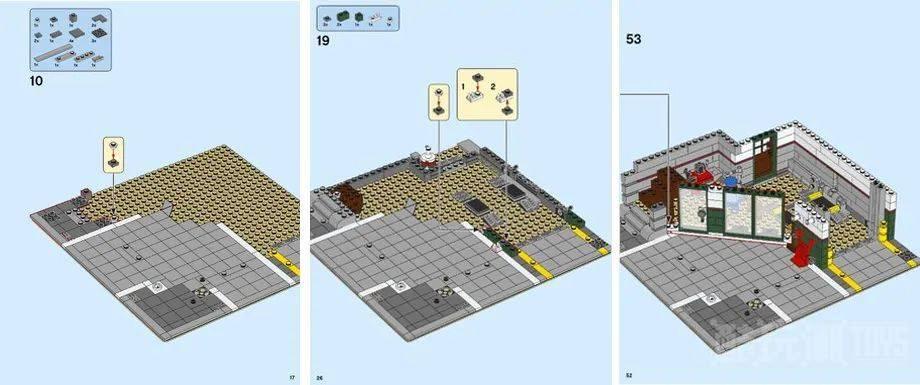
如果我们将此视为直角三角形的斜边，则其他两侧各有 12 个颗粒长（如果您想象从两个连接点处的颗粒沿乐高网格绘制的水平和垂直线，它们将相交颗粒在每个方向上相距 12 个颗粒）。
现在我们来看，(12,12,17) 严格来说不是勾股定理三元组。但是直角三角形的斜边的长度是 √(12² + 12²) = 16.97，它足够接近 17。1×2 圆板就像铰链一样，提供牢固的连接，同时允许一点回旋的余地。
“三倍数”也以 45 度角（相对于底板）连接遮阳篷的方式发挥作用。但是这里的数学是如何工作的并不那么明显。仔细观察，我们看到遮阳篷是 16×10 颗粒宽，圆角。它使用铰链组件连接到车库的斜墙上，该铰链组件由顶部有一根手指的 1×3 光面砖（连接到斜墙上）和带有两个圆角 1×2 板（并入遮阳篷本身）组成）。
遮阳篷由使用十字轴和轴连接器创建的两个垂直柱支撑。这些柱子将遮阳篷连接到加油站，但加油站本身仅在一个位置与基地相连。这样的搭建，就显得更加的合理了。
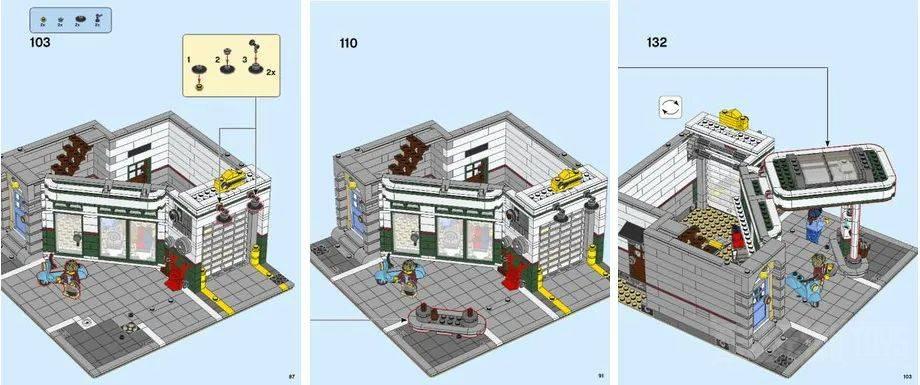
加油站岛有两个 4×4 圆板，它们相隔 6 个颗粒（中心到中心），但鉴于没有“三倍数”，最大的 6 个，因此无法以 45 度角连接它们数字。所以设计师选择将加油站岛的一侧连接到一个带孔的 2×2 光面板上（这连接到 4×4 圆板的底部形成一个转盘），另一侧不连接（它只是休息在 2×2 黑色转盘底座上）。
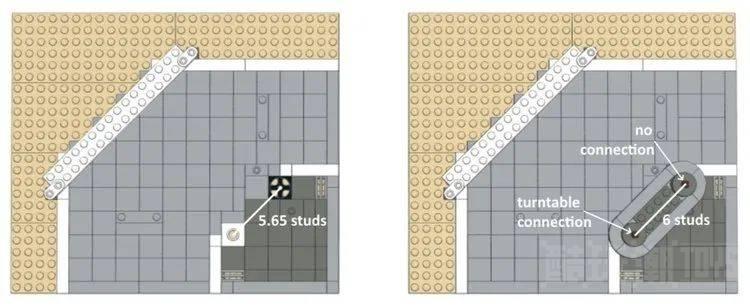
我们可以看看实际有连接的那一面，并尝试找出其中涉及的数学原理。连接点距离连接倾斜立面末端的线正好 13.5 个颗粒。这可以分为两个“接近三元组”。首先，我们从代表原始“三倍数”（12,12,17）的直角三角形开始。
如果我们从与最长边（或斜边）相对的顶点（角）画一条线，使其与斜边成直角相交，我们将得到两个尺寸相同的直角三角形（8.5,8.5,12）。这也是一个“近三倍”，所以我们可以认为 13.5 中的 8.5 是这个较小直角三角形的一条腿（较短的边）。剩下的 5 个是另一个“三倍数”（3.5,3.5,5）的斜边（最长边）。很酷，对吧！？
使用圆盘零件制作出一个圆形
转盘也可以以其他有趣的方式使用，例如创建圆形。2022年4月，乐高宣布为其植物系列产品线新增两款产品。下面我就以今年刚刚发布的10311 兰花套装为例。各位肯定想不到，在一个有花的套装中可能会涉及到什么样的数学？
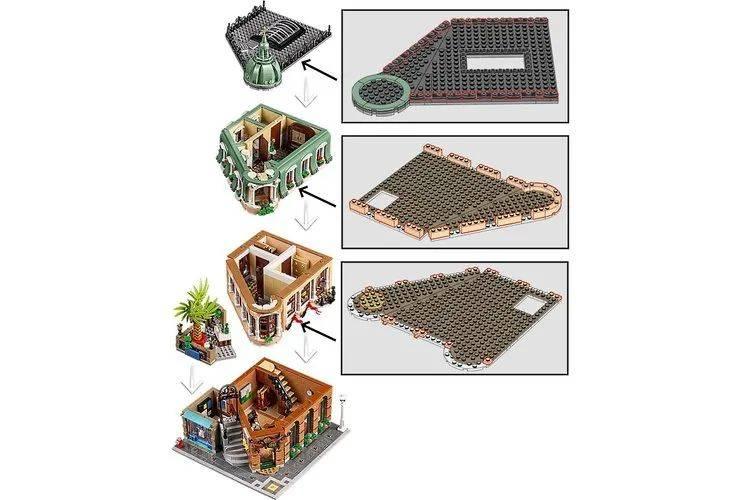
如果你猜对了我说的是花瓶，当然可以加分！乍看之下，凹槽花瓶是如何组合在一起的，它的完美圆形和双斜面连在一起，几乎没有任何间隙，它们之间几乎是奇迹般的存在。
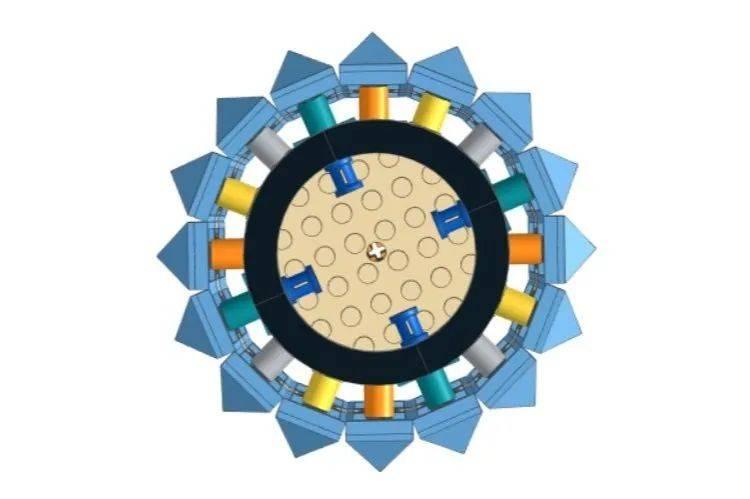
当我看到兰花套装的公告时，花瓶是第一个引起我注意的东西（尽管我不得不承认它的其余部分也很整洁）。但是使用乐高创建圆形并不是那么容易。兰花套装的设计师Mike Psiaki提出了一个非常聪明的方法，它主要依赖于 8×8 圆盘的数学特性进行创作，现在我们看看他是怎么做到的。
8×8 圆盘是乐高目录中一个相对较新的零件，加入了它的较小兄弟姐妹（例如 4×4 和 6×6 圆盘）的行列里。但是关于 8×8 圆板的一个巧妙之处在于，其外围的所有颗粒与板边缘的距离大致相同，这包括沿对角线的颗粒。这不适用于 6×6 圆板，其中沿对角线的颗粒从板的边缘稍微插入一点。
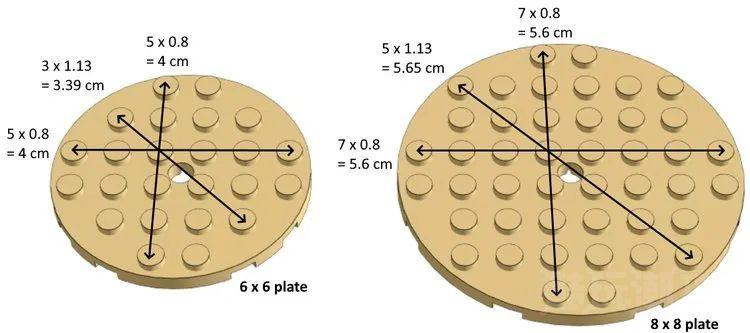为了理解原理，让我们考虑两个颗粒之间的对角线距离，它是颗粒尺寸（0.8 厘米）的 √2 倍，等于 1.13 厘米。在 6×6 圆板上，沿对角线的最外侧颗粒之间的距离为 3 x 1.13 = 3.39 cm = 4.24 颗粒，而在 8×8 圆板上它是 5 x 1.13 = 5.65 cm = 7.06 颗粒，非常接近沿水平轴和垂直轴的最外侧颗粒之间的 7 颗粒间距。
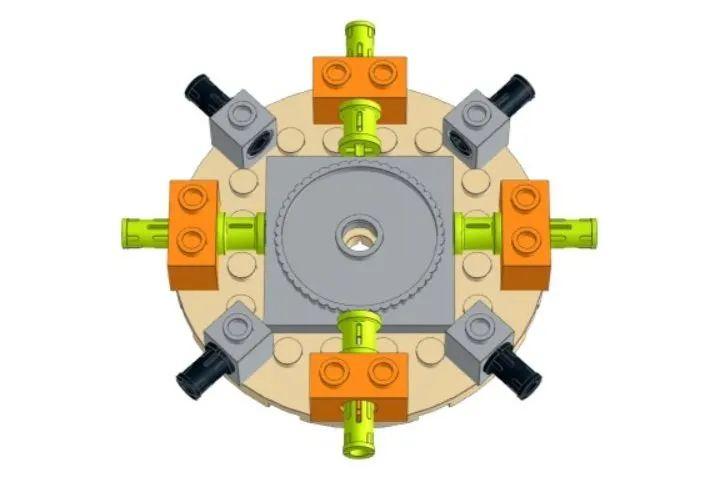这使我们能够做的是沿着 8×8 圆板的外边缘放置机械孔砖，并在所有侧面突出大约相同数量的机械销零件。当然，沿对角线的 1×1 机械孔砖积木需要旋转 45 度角。8×8 圆盘带有 8 个32054 十字轴孔长栓，这只是使用转盘堆叠和旋转的四层之一，以构成花瓶的核心。
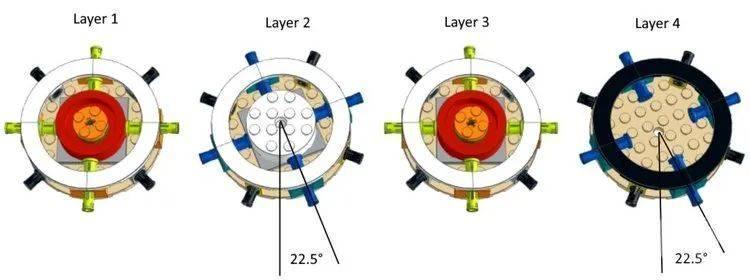
偶数层（第 2、4 层）的旋转角度是 45 度或 22.5 度的一半。这会将偶数层上的八个机械孔砖的基座位置恰好位于奇数层上的八个机械孔砖的基座位置之间。当所有四层都堆叠起来时，我们总共有 16 列机械孔砖的基座，沿着核心的圆周均匀分布。
16 个机械件1×7 提升臂件可以连接到这些机械销上，这样我们就可以连接创建凹槽外观所需的双斜面件。请注意，在顶部添加 4×4 通心粉光面板时，每层的高度为 5 个板，这确保了堆叠层时机械孔砖的基座之间的正确垂直间距。
为什么我们甚至需要机械孔臂零件？为什么不使用 SNOT 积木，或者不是科技件积木并将双坡块直接连接到它们之上？我们再次需要一些数学逻辑来帮助解释这一点。8×8圆板的直径为8个螺柱或20个板。将机械孔臂（与普通砖的高度一样厚）连接在两侧，总直径变为 20+3+3=26 个板。
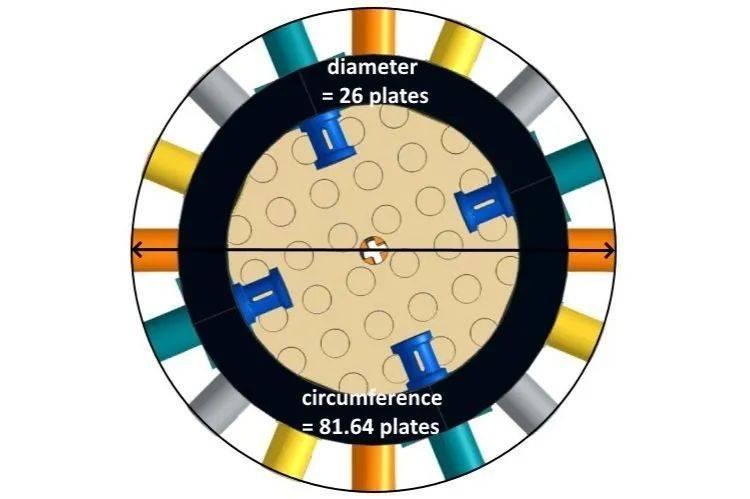
核心的周长现在是 π x 26 = 81.64 个板。现在将它除以 16，你得到 5.1 个板，它非常接近每个双斜块的 5 个板（2 个颗粒）宽度。现在我们看到提升臂部件如何帮助使内核足够大以将双斜度部件连接到周围，它们之间几乎没有间隙
结束语
小编希望本文能成功激发您对隐藏在您使用乐高构建的所有东西背后的数学的兴趣。只要你不介意用一点枯燥的数学来解决搭建过程中的难题，你可以从官方乐高套装中学到很多很酷的技术，当你设计自己的 MOC 时，它们甚至可以派上用场。说到 MOC，我希望在后续文章中至少介绍其中的一些。同时，如果官方乐高套装中使用的任何技术仍然让您摸不着头脑，请随时在此处发表评论。最后，祝各位都有一个能让自己身心愉悦的搭建体验！
····· End ·····
评论